Reta Tangente e Normal a Curva
Produzido por Mariana PessanhaTeoria
Equação da reta tangente
Imagine que nos deparamos com o seguinte problema:
Encontre a reta tangente da curva no ponto .
Para resolver essa questão, vamos fazer o seguinte passo a passo:
- Encontrar correspondente ao ponto :
- Calcular :
- Calcular :
- Temos um vetor tangente a curva e o ponto de tangência . Logo, basta montar a equação da reta tangente:
- Encontrar correspondente ao ponto ou vice-versa
- Calcular
- Calcular
- Substituir em , que é a equação da reta tangente.
- Encontrar correspondente ao ponto ou vice-versa
- Calcular
- Calcular
- Calcular
- Substituir em
- Encontrar correspondente ao ponto :
- Calcular :
- Calcular :
- Calcular :
- Substituir:
Comparando a terceira componente:
De maneira geral, o nosso passo a passo vai ficar:
Equação da reta normal
Assim como a gente pode encontrar a reta tangente a uma curva , podemos também encontrar uma reta normal a ela.
Beleza, mas como?
Exatamente do mesmo jeito que encontramos a reta tangente. Mesmo passo a passo, só que agora, usamos o vetor normal!
Beleza, sabemos então que a equação paramétrica da reta é dada por:
Onde é um ponto da reta e é um vetor na direção da reta.
Quando queremos encontrar a reta normal a uma curva, sabemos que o ponto pertence à reta e que o vetor está na direção da reta normal.
Opa! Então a reta normal à curva em é dada por:
Simples assim!
Vou te dar um passo a passo então pra ficar ainda mais simples:
Exemplo:
Encontre a reta normal a curva no ponto .
Comparando as três coordenadas:
Mole?
Agora vou te dar duas dicas muito importantes:
- Qualquer vetor pode ser obtido pela diferença entre dois pontos! Assim, se sabemos que nosso vetor normal passa por um ponto , para encontrar o vetor normal basta subtrair esse ponto de um outro ponto genérico .
- Para descobrir quem é esse ponto genérico, precisamos lembrar que o vetor normal é perpendicular ao vetor tangente e que o produto escalar entre dois vetores perpendiculares é nulo.
Assim, sabendo o vetor tangente a curva em , fazemos o produto escalar entre ele e o e encontramos o ponto .
Depois é só substituir em
Por exemplo:
Seja
O vetor tangente uma curva no ponto da curva.
O vetor normal a essa curva, neste mesmo ponto, será:
Tal que
Agora podemos escolher qualquer valor de e que satisfaçam essa equação.
Vamos escolher e .
Assim, nosso vetor normal será:
Agora é só substituir em
Tranquilo, né? Partiu exercícios então!
Exercícios Resolvidos
Exercício Resolvido #1
Hamilton Luiz Guidorizzi, Um curso de cálculo, Volume II, 5ª ed. Rio de Janeiro: LTC, 2001, pg.134, exercício 2b.
Encontre a equação da reta tangente à trajetória dada, no ponto dado:
Passo 1
Tanquilo, tudo o que temos que fazer é seguir aquele passo a passo que te dei lá na teoria:
Encontrar ao ponto G correspondente a :
Aqui temos
Logo,
Então:
Passo 2
Calcular :
Passo 3
Calcular G:
Passo 4
Substituir em
Resposta
Exercício Resolvido #2
Apostila aprendendo cálculo de várias variáveis, Professor Waldecir Bianchini, exemplo 3.8
Determinar as equações paramétricas da reta tangente à elipse:
no ponto:
Passo 1
Neste caso, não temos a curva parametrizada, então precisamos parametrizar a elipse:
Então:
Então nossa curva fica assim:
Passo 2
Encontrar correspondente ao ponto ou vice-versa:
Neste caso, o problema deu o ponto, então devemos encontrar :
Igualando as duas coordenadas:
Como só tem funções trigonométricas na curva parametrizada, nem precisamos determinar o valor de , basta saber os valores do seno e cosseno!
Passo 3
Calcular :
Passo 4
Calcular :
Passo 5
Reta tangente:
Substituir em :
Resposta
Exercício Resolvido #3
UFRJ, Calculo Diferencial e Integral 2, P1 2014.2, exercício 3, múltipla escolha
Considere a curva parametrizada por , onde é uma constante. Para que valor de a reta tangente a no ponto passa pelo ponto ?
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos calcular a equação da reta tangente a no ponto , basta seguir o passo-a-passo!
Primeiro vamos encontrar o no qual :
Então vamos ter o sisteminha
Passo 2
Beleza, agora temos que calcular . Com a regra da cadeia, temos
Portanto,
Passo 3
Show! Agora vamos achar
Passo 4
Então a equação da reta tangente a em , para um genérico, é:
Queremos que a reta passe pelo ponto , então
A primeira equação dá . Substituindo na segunda, obtemos
Resposta
Alternativa (e)
Exercício Resolvido #4
PUC-RJ, Calculo 3, P1 2012.2, questão 2
O movimento de uma partícula no intervalo de tempo é descrito pela curva parametrizada .
a) Encontre a equação paramétrica da reta tangente a curva no instante .
b) Suponha que no instante a partícula sai pela tangente em movimento retilíneo uniforme. Ache a posição da partícula no instante .
Passo 1
Aqui temos que encontrar a equação paramétrica da reta tangente. Para isso, precisamos saber antes de mais nada qual é o ponto para o parâmetro ! Substituindo esse valor na equação da trajetória, teremos:
Beleza, então queremos a reta tangente no ponto !
Passo 2
Agora, vamos encontrar o vetor diretor da reta tangente, que é o vetor derivada da função da curva.
Para , o vetor é:
E o vetor diretor da nossa reta é
Passo 3
Agora que temos o ponto e o vetor diretor, basta colocar na equação da reta!
E pronto, aí está :D
Passo 4
Para saber a posição da partícula que agora anda seguindo a equação da reta, basta colocar o parâmetro que corresponde a ! Como a equação de começa em , que é quando está em , então existe um “atraso” de entre os parâmetros, percebe? Assim, quando estamos em , estamos em , pegou a ideia?
Colocando , teremos:
Resposta
a) A equação da reta é
b) O ponto é
Exercício Resolvido #5
UFRJ, Calculo Diferencial e Integral 2, P1 2014.2, questão 1
Considere as duas superfícies dadas por e .
1. Esboce, separadamente, as duas superfícies, mostrando as curvas de interseção com os planos coordenados.
2. Parametrize a curva obtida pela interseção das 2 superfícies.
3. Calcule a reta tangente a no ponto .
4. Existe algum ponto de no qual a reta tangente passe na origem? Justifique.
Passo 1
1.
Vamos focar na primeira superfície, beleza?
Ela é dada por
então temos algo do tipo
portanto, essa superfície é um plano :)
Passo 2
Agora vamos ter que esboçar a figura, mostrando suas interseções com os planos coordenados. Então vamos pôr a mão na massa!
Vamos zerar uma a uma as coordenadas , e e assim determinar como o nosso plano intercepta os planos , e , respectivamente. Vamos fazer um desenho e ir completando aos poucos, beleza? Então partiu!
Fazendo vamos ter a reta
e
Então, no plano , a reta passa pelos pontos e .

Passo 3
Fazendo temos a reta
e
Ou seja, a reta passa pelos pontos e .
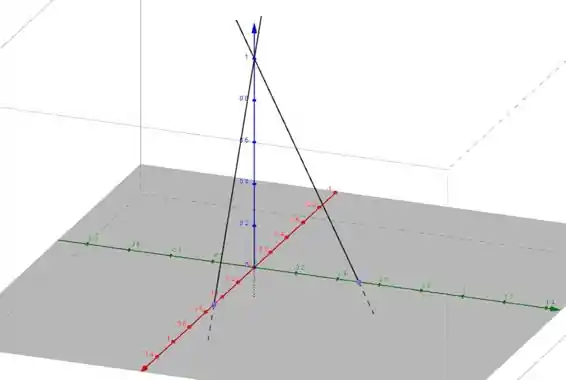
Passo 4
Fazendo temos:
e
Então a reta passa pelos pontos e . Vamos completar de novo o desenho:
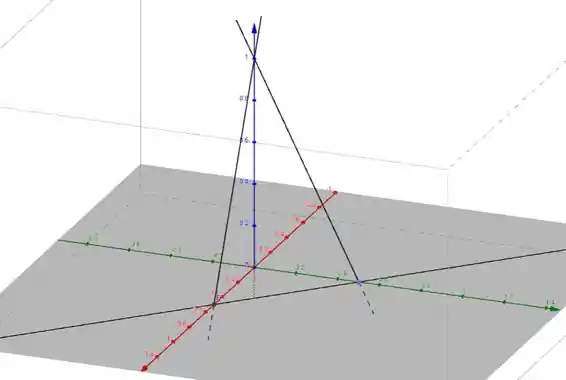
Passo 5
Então esse triângulo daí é composto pelas retas de interseção do nosso plano com os planos coordenados Ele vai ser a base do esboço do plano:
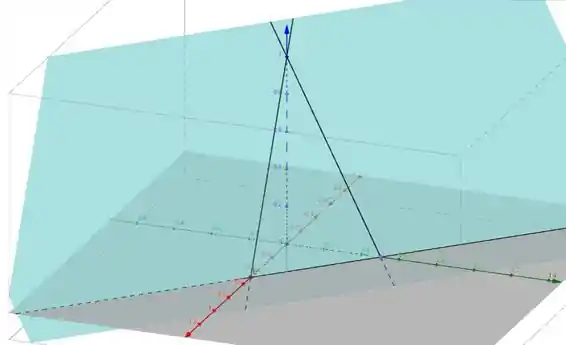
Desse ângulo dá pra ter uma visão melhor:
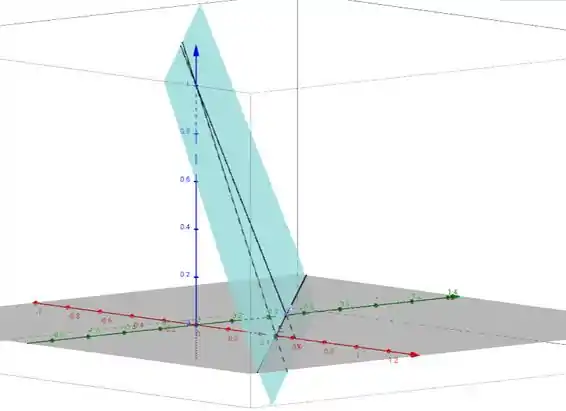
Passo 6
Ainda temos a outra superfície!
A equação dela é:
Isolando o fica:
Identificamos uma superfície do tipo
que nada mais é que a equação de um paraboloide!
- Os dois sinais são iguais, então a superfície é um paraboloide elíptico.
- Como , vai ser mais precisamente um paraboloide circular.
- Os sinais são positivos, então ele vai ser virado pra cima.
- O valor mínimo de e é , então o mínimo absoluto e vértice do paraboloide é no ponto .
Excelente! Já da pra ter uma boa noção da figura :D
Passo 7
Agora vamos determinar as curvas de interseção do paraboloide com os planos coordenados:
- No plano , temos
que é uma parábola voltada para cima e com mínimo em .
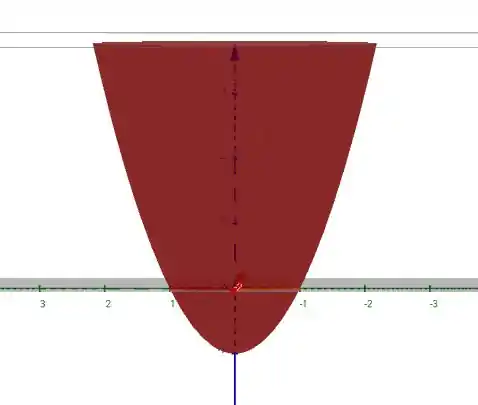
- No plano , a equação fica
que é exatamente a mesma parábola do item anterior, só passando do plano pro plano .
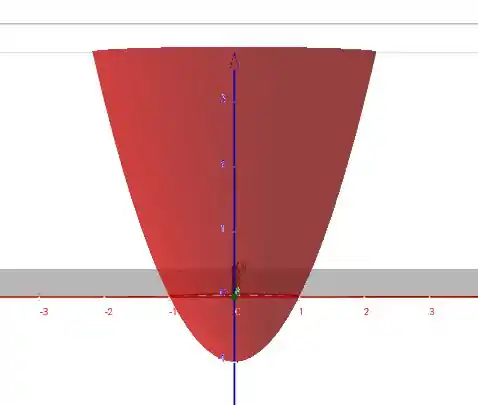
- No plano , temos
que é um círculo de raio 1 centrado em .
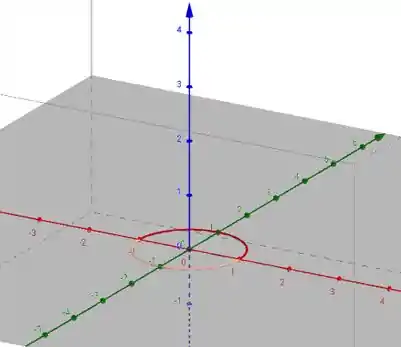
Passo 8
Juntando tudo, obtemos o nosso paraboloide!
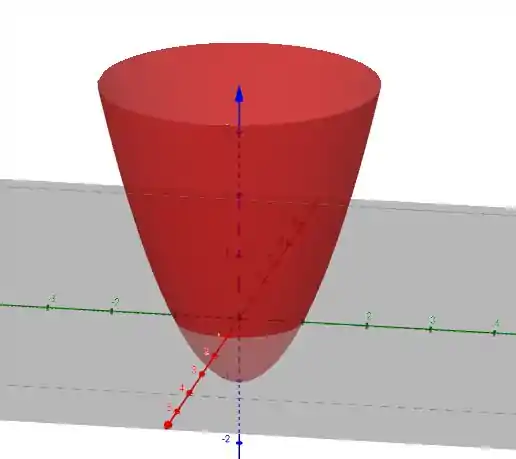
Beleza, podemos continuar!
Passo 9
2.
Agora temos que parametrizar a interseção das duas superfícies, que foi chamada de . Vamos seguir o passo a passo pra esse tipo de questão:
- Isolar uma variável de uma das equações
- Substituir na equação da outra superfície
- Parametrizar essa projeção da curva com as outras duas variáveis
- Substituir essas parametrizações na terceira variável que foi isolada
Passo 10
Na equação do paraboloide, já está isolado, então vamos usá-lo!
Substituindo na equação do plano, temos:
Completando quadrados:
E a equação de um círculo de centro e raio é:
Então a projeção de no plano é o círculo de centro e raio , tranquilo?
Passo 11
Agora temos que parametrizar essa projeção. Como é um círculo, vamos usar algo do tipo e pra gente usar e abusar da relação: .
Então vamos fazer isso:
Pra eliminarmos esse e , podemos escolher . Então vamos ter:
Para ter algo multiplicando podemos fazer . Assim:
Então, uma parametrização possível pra esse círculo é:
Passo 12
Show! Agora só falta substituir essa parametrização na variável :
Logo, uma parametrização de é:
Passo 13
3.
Agora queremos a reta tangente a no ponto . Beleza, precisamos descobrir em que temos :
O que nos dá um sistema:
Pela primeira equação:
Como :
Se quiser, você pode verificar que as outras equações são respeitadas :)
Passo 14
Pra achar a reta tangente em , vamos precisar de . Então vamos começar calculando :
Então em temos:
Logo, uma parametrização da reta tangente a em é:
Passo 15
4.
Enfim, pra finalizar essa pergunta gigante, ele nos pergunta se existe um ponto de onde a reta tangente passa na origem.
Na verdade, vai ser até simples de responder.
Vejamos, por definição a curva está contida no plano . Então qualquer reta tangente a um ponto de deve estar contida no plano! Ele é 2D, a reta tangente não pode simplesmente sair por aí!
E como a origem não está no plano, nenhuma reta tangente de pode passar nela!
Então é isso, fechamos a questão! (Aleluia!!)
Resposta
1.
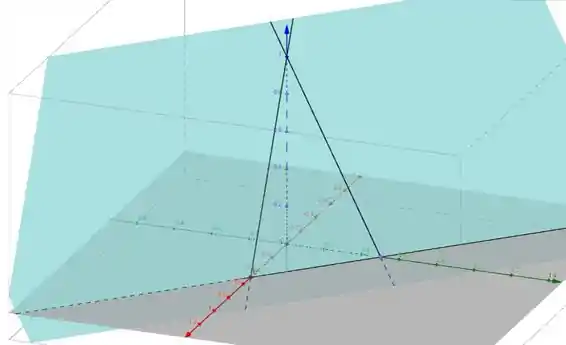
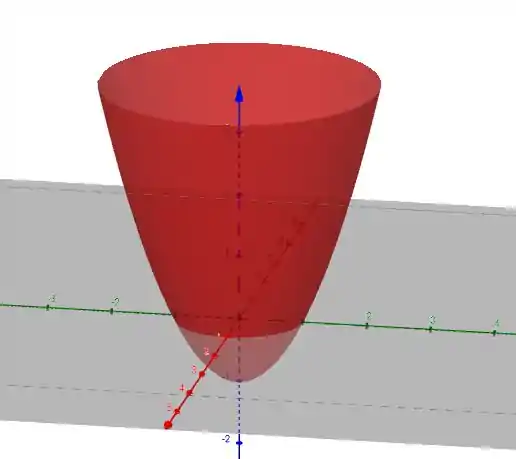
2.
3.
4.
Não.
Exercício Resolvido #6
UERJ, Análise Vetoria, Lista Profª Joice, questão 5b
Encontre a equação paramétrica da reta normal à curva
no ponto .
Passo 1
Para encontrar a equação da reta normal, precisamos primeiro do vetor tangente, porque é o mais proximo que conseguimos com as informações que o enunciado nos deu.
Comecemos por encontrar qual é o valor do parâmetro para o ponto dado. Para, isso, basta igualar o ponto a equação da reta
Passo 2
Agora, vamos derivar a equação para descobrir o vetor tangente
Para derivar uma equação paramétrica, basta derivar cada um de seus componentes!
Passo 3
Agora colocamos o valor do parâmetro, calculado no passo 1, na equação da derivada e achar quais são as componentes do nosso vetor tangente
Passo 4
Agora que temos o vetor tangente, podemos encontrar facilmente o vetor normal. Para isso basta saber que qualquer vetor pode ser obtido pela diferença entre dois pontos!
Sabemos que o vetor normal passa pelo ponto , logo, podemos subtrair este ponto de um outro genérico , que ainda vamos descobrir. Então, nosso vetor normal fica
Viu como é simples??
Passo 5
Como o vetor tangente é perpendicular ao vetor normal, e o produto escalar entre vetores perpendiculares é 0, agora podemos matar a questão!!
Encontramos uma reta na qual o nosso vetor está contido!! Agora é só escolher um ponto dela e fazer a subtração do ponto para encontrar o vetor!!
Passo 6
É muito conveniente escolher um ponto onde uma das coordenadas seja 0, apenas pra fazer menos conta mesmo. Veja, quando temos ....
Ou seja, o ponto está sobre a reta e pode ser um dos extremos do nosso vetor.
Passo 7
Fazendo agora o vetor, basta subtrair o ponto encontrado no passo anterior do nosso ponto da curva.
Temos então que:
Mas, pra não ficar levando esse sinal de menos por resto, vamos multiplicar esse vetor por : assim, alteramos o sentido, mas não a direção do vetor, que é o que importa! Então,
Passo 8
Usando a fórmula da reta para quando temos um ponto e um vetor, conseguimos, agora, parametrizar a reta normal à curva!
Resposta
Encontramos, então, a reta
Exercício Resolvido #7
UERJ, Análise Vetoria, Lista Profª Joice, questão 5a
Determine a reta normal da curva
no ponto correspondente a
Passo 1
Vamos determinar a reta normal exatamente como o plano normal em Cálculo 2! A diferença é que como estamos num mundo 2D, dessa vez nao teremos um plano, mas uma reta, porque perdemos uma dimensão!
Primeiro, comecemos encontrando esse ponto de tangência. Basta colocar o parâmetro dado na equação da curva!
Assim, nosso ponto é
Passo 2
Agora, vamos derivar a equação e encontrar o vetor tangente a reta quando o parâmetro é
Passo 3
Colocando o parâmetro, fica...
Assim, nosso vetor tangente à curva no ponto dado é
Passo 4
Perfeito! Agora temos o vetor tangente à curva no ponto que calculamos. Para encontrar a reta normal à curva, basta encontrarmos o vetor perpendicular ao vetor tangente!
Podemos definir um vetor como a diferença entre dois pontos. Portanto, como não sabemos qual é esse vetor normal, mas sabemos que ele passa pelo ponto , vamos subtrair este ponto de outro, genérico, que ainda vamos descobrir. Assim, nosso vetor normal é
Passo 5
Agora podemos fazer que o produto escalar entre o vetor tangete e normal é 0, pois são perpendiculares:
Continuando a resolver a equação....
Esse resultado nos diz que qualquer ponto sobre a reta pode ser candidato para outra extremidade do nosso vetor! Perceba que o ponto também está nessa reta!! Existem milhões de vetores equivalentes, pasta pegar dois pontos dessa reta e diminuir um do outro!
Passo 6
Vamos, então, parametrizar (esticando ele, pra virar uma reta) nosso vetor (muito simples mesmo)
Como , podemos parametrizar assim:
porque e tem sempre o mesmo valor!!
Passo 7
Para definir uma reta precisamos apenas de um ponto e de um vetor! Pela definição, temos que esticar esse vetor (parametrizando-o), e depois somar um ponto por onde essa reta passe:
Como ja temos o vetor normal esticado, basta somar a ele o ponto por onde deve passar,