Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 56

  1. Mostre que a equação da reta tangente à parábola y 2 = 4 p x no ponto x 0 , y 0 pode ser escrita como y 0 y = 2 p ( x + x 0 )
  2. Onde essa reta tangente intercepta o eixo x ? Use esse fato para desenhar a reta tangente.

Passo 1

Olá, meu amigo. Vou te ajudar a resolver essa atividade.

A primeira coisa que nos é pedido aqui é para provarmos que a equação da reta tangente a parábola de forma:

y 2 = 4 p x

No ponto:

( x 0 , y 0 )

Pode ser escrita como:

y 0 ⋅ y = 2 p x + x 0

Para encontrarmos essa reta, deveremos lembrar que a inclinação de uma reta tangente a uma curva é dada por:

m = d d x ( y )

E que a equação da reta tangente que passa por um ponto ( x 0 ,   y 0 ) e tem inclinação m é dada por:

y - y 0 x - x 0 = m

Após derivarmos a nossa função, teremos então o m e a aí é só substituirmos.

Passo 2

  1. A equação de uma reta com inclinação 2 p y 0 e passando por x 0 , y 0   é

    2. y - y 0 x - x 0 = 2 p y 0

    y 0 y - y 0 = 2 p ( x - x 0 )

    y 0 y - y 0 2 = 2 p ( x - x 0 )

    Da equação da parábola sabemos que y 0 2 = 4 p x 0 , então vamos substituir:

    y 0 y - 4 p x 0 = 2 p ( x - x 0 )

    y 0 y = 2 p x - x 0 + 4 p x 0

    y 0 y = 2 p x - x 0 + 2 x 0

    y 0 y = 2 p x + x 0

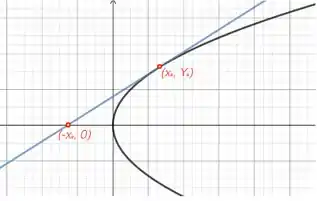
  2. Queremos encontrar o ponto onde essa reta tangente corta o eixo x , bom, para isso podemos usar nossa equação do item (a), com y = 0 :

y 0 y = 2 p x + x 0

y 0 ( 0 ) = 2 p x + x 0

0 = x + x 0

x = - x 0

Então nossa reta intercepta o eixo x no ponto ( - x 0 , 0 ) . Assim, podemos fazer o desenho:

Resposta

a) Demonstração

b) ( - x 0 , 0 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes17. r = c o s 2 θ
Nos exercícios de 21 a 28, ache χ e α para a curva dada no ponto cujo valor de θ é o indicado. Faça um esboço da curva e mostre χ e α .23. r = s e c 2 θ ; θ = - π 8
Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes20. r 2 = 9 c o s 2 θ
Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes19. r 2 = 4 s e n 2 θ
Nos exercícios de 1 a 8, ache a inclinação da reta tangente à curva dada no ponto, cujo valor de θ é o indicado. Faça também um esboço do gráfico e da reta tangente.6. r = 3 - 2 c o s θ ;θ = 2 π 3