Derivada Por Definição
Produzido por Arthur Melo de AlmeidaTeoria
A derivada de uma função é a taxa de variação instantânea de
Bora ver como isso funciona?!
Como Calcular a Derivada por Definição
Para calcular a derivada por definição, usamos essa fórmula aqui:
Bora entender o que isso significa?! 🤩
📢 Clique para saber mais:
- Derivada por Definição: Exercícios Resolvidos
- Derivadas Primitivas
- Tabela de Derivadas
- Calculadora de Derivadas
Derivada de um Ponto
Antes de qualquer coisa a gente precisa entender que a derivada é uma taxa de variação! Pra a gente entender na prática como isso funciona, se liga nos pontos
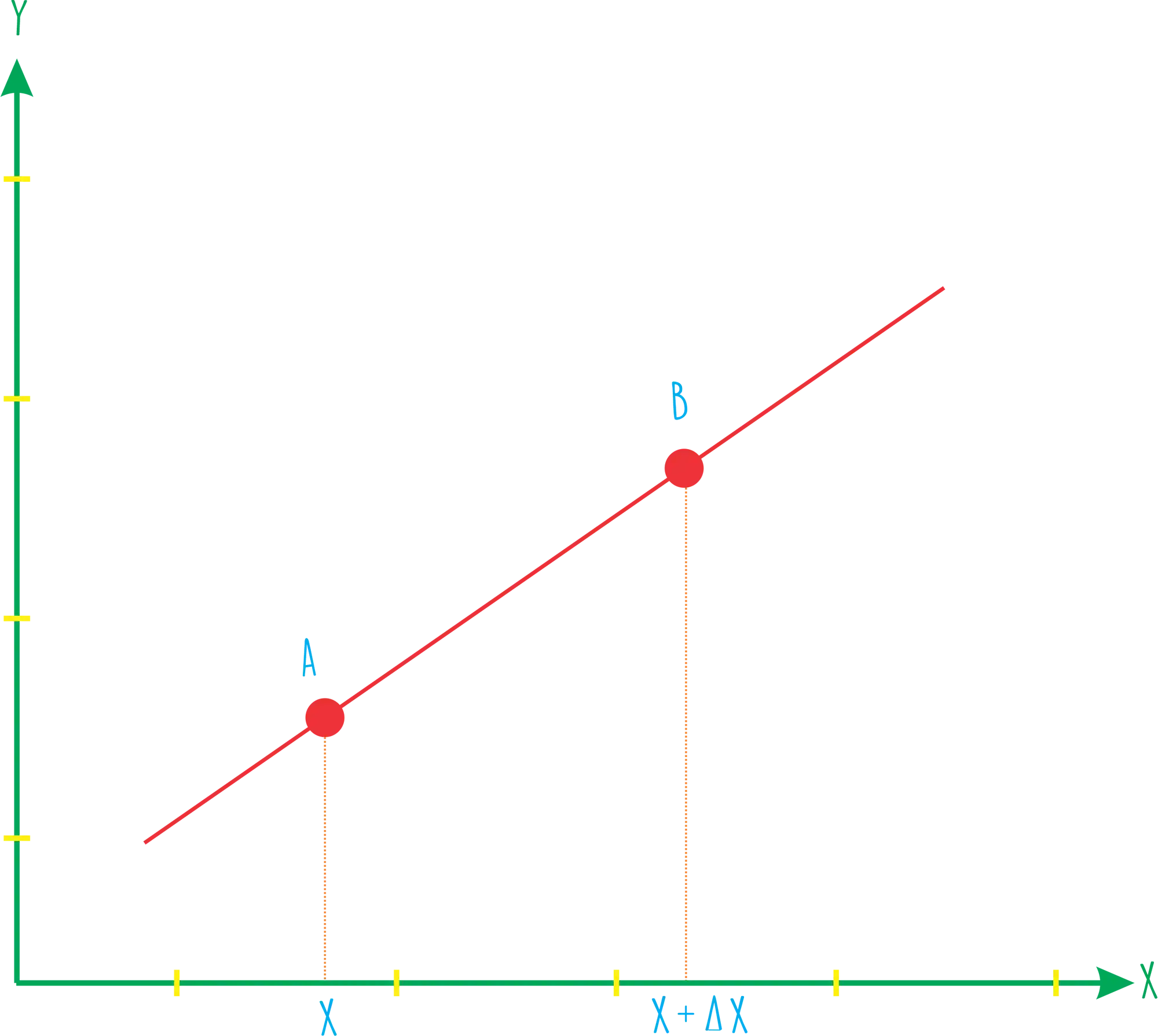
Imagina que queremos saber qual é a taxa de variação da função acima, entre os pontos
Esse
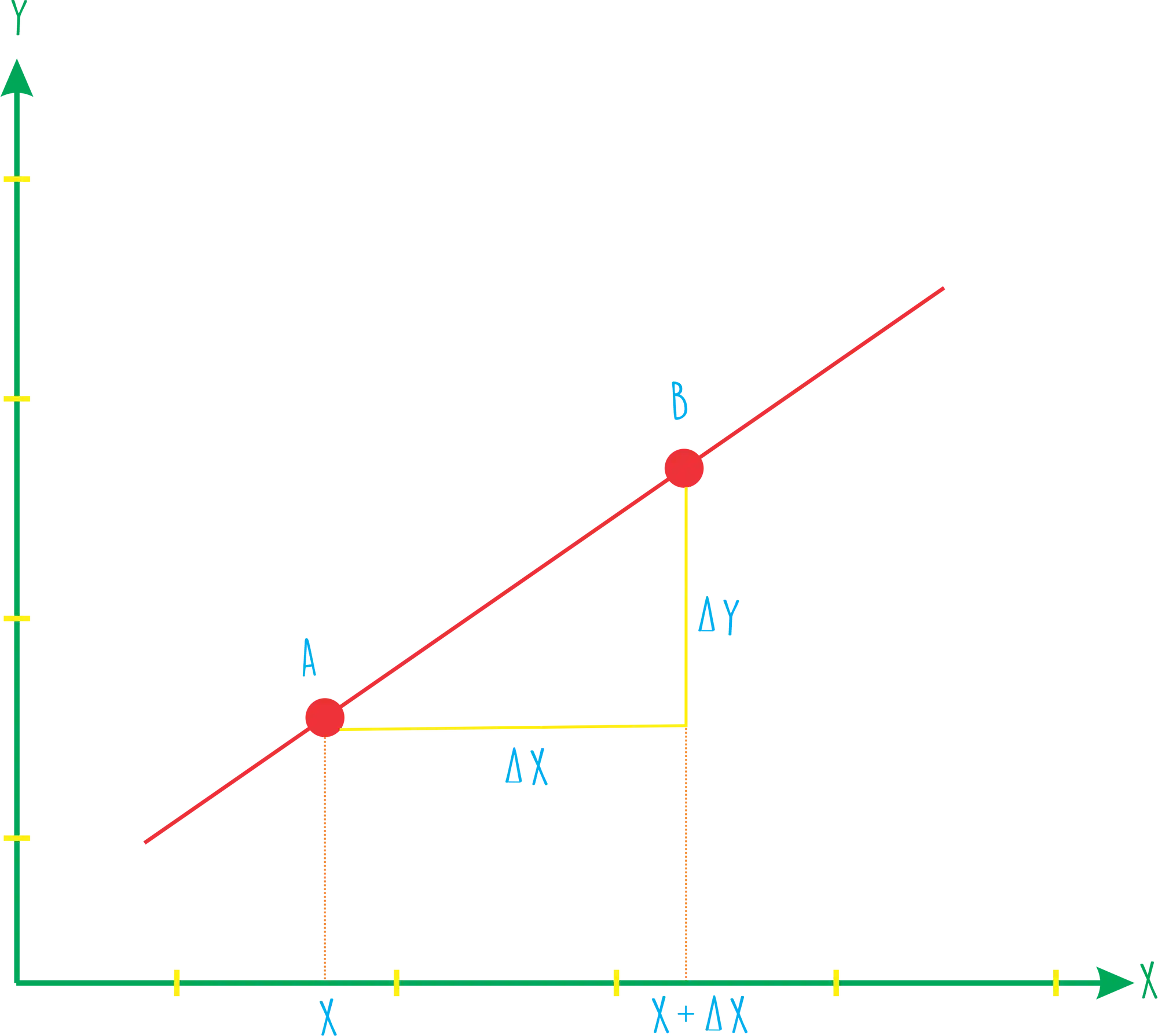
Podemos escrever da seguinte forma:
Isso lembra a fórmula de inclinação da reta, não é? É isso mesmo! Agora a gente pode reescrever da seguinte forma:
Mas se esse
Você terminou de conhecer a derivada por definição! 🥰 Representamos ela assim:
Você também pode conferir esse conteúdo em vídeo:
Exemplo: Calcule a derivada de
Para calcular a derivada, precisamos saber a expressão para a função no ponto
Agora, vamos substituir isso na nossa expressão de definição de derivadas:
Podemos cortar o
E pronto, encontramos a derivada! Agora vamos praticar com exercícios?