Se um tanque cilíndrico comporta litros de água, que podem escoar pela base do tanque em uma hora, então a Lei de Torricelli fornece o volume de água que restou no tanque após minutos como:
Encontre a taxa pela qual a água está escoando para fora do tanque (a taxa instantânea da variação de em relação a ) como uma função de . Quais são suas unidades? Para os instantes e minutos, encontre a taxa do escoamento e a quantidade de água restante no tanque. Resuma o que você achou em uma ou duas sentenças. Em que instante a taxa do escoamento é máxima? E a mínima?
Passo 1
E aí pessoal, beleza?

Essa questão aqui é beeeem bacana, mostra a aplicação de derivada de uma forma bem contextualizada, relacionando a taxa de variação com o escoamento de um tanque!
Temos uma fórmula para volume de água em um tanque que esta sendo escoado:
A partir disso o enunciado pede várias coisinhas! Na primeira temos que calcular a taxa de variação instânea de em função do tempo.
Pra responder isso vamos precisar lembrar da definição de derivada. Teremos que a derivada será dada por:
O que queremos e precisamos achar é justamente esse cara, o . Já sabemos quem é o (que é dado para a gente no enunciado), agora acharemos o , fechou?). Olha como vai ficar:
Vamos substituir, agora, e na expressão de :
Veja só! 😎
Passo 2
A próxima etapa e arrumar a nossa função, de uma forma que fique mais fácil da gente resolver o limite. Vamos começar reescrevendo ela dessa forma aqui:
Dentro dessa expressão nós temos produtos notáveis na forma quadrado da diferença: o primeiro é o e o segundo o . Expandido esses produtos notáveis, vamos ter:
Fazendo o jogo de sinas com o par��ntese maior do lado direito:
Agora, vamos expandir os termos elevados ao quadrado:
Simplificando agora com nas frações em que podemos fazer isso, vai ficar assim:
Agora a gente vai juntar os caras que tem o mesmo denominador em comum! Vai ficar assim, saca só:
Fazendo as subtrações possíveis, vamos ficar com essa expressão aqui:
Pronto! Agora ela ta bem mais arrumada e podemos trabalhar melhor com ela!
Tranquilo até aqui? 😬
Passo 3
Agora, precisamos resolver o limite em desse exercício. Se fizermos a substituição na tentativa de resolver esse limite, cairemos em uma indeterminação . Para resolver ess problema, podemos deixar o do numerador em evidencia e cancelar com o do denominador, beleza? Olha só o que eu quero dizer:
Pronto, dessa forma ai que tá, já podemos resolver o limite! Agora vamos fazer a substituição :
Tirando o MMC das nossas frações, vai ficar assim:
E dando mais uma arrumadinha:
Pronto! Essa é a nossa taxa instantânea de variação, em , em função do tempo .
Se você já resolveu bastante exercício de limite, no final do passo é bem capaz de ter sacado que ia aparecer essa determinação e precisava colocar o em evidência. Esse tipo de situação é bem comum ao se trabalhar com limite, então guarda logo essa dica aí viu!
Estamos quase lá! 😉
Passo 4
Agora, temos que calcular o volume restante no tanque e a taxa de escoamento para e minutos. Tudo que precisamos é substituir os valores de nas expressões de e , ta tranquilo? Fizemos essa tabela aqui com os valores encontrados nas contas, olha só:
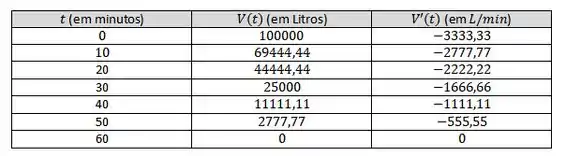
A partir da tabela, podemos concluir algumas coisas. É possível ver que a taxa de variação é sempre negativa – isso indica que o volume no tanque diminui com o tempo, de acordo com o esperado!
Outra coisa: conforme o tempo passa, a intensidade, a magnitude da taxa de variação vai ficando menor. Isso quer dizer que no início a água saí muito mais rápido que no final, quando a vazão é menor, beleza? Daí a gente tira que quando temos a taxa de variação de maior magnitude e quando a de menor magnitude.
Pronto, respondemos todo o exercício! Esse é trabalhoso mas é bem legal mesmo, então dá uma estudada legal nele que vai te ajudar a ficar fera em derivada! ;)
O que achou? Responde Aí! 😉

Resposta
A taxa com a qual a água escoa de acordo com o tempo é dada pela expressão:
Para os instantes e minutos, temos os seguintes volumes e taxas de escoamento:
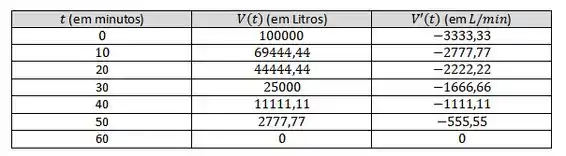
É possível ver que a taxa de variação é sempre negativa – isso indica que o volume no tanque diminui com o tempo. Logo, a taxa de variação com maior magnitude acontece quando e a de menor magnitude quando .