Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

EDO Exata

Ver Todos os Exercícios

Teoria

Opaa, seja muito bem vindo ao Responde Aí! Bora bater um papo sobre EDO exata?! 😉 👇

O que é uma Equação Diferencial Exata?

Segundo o critério de Euler, uma EDO é exata se puder ser escrita da seguinte forma:

Onde:

Não entendeu nada? Bora ver um exemplo então! Vamos considerar a seguinte EDO:

Só de olhar a carinha dessa equação, podemos perceber que ela é de primeira ordem, afinal sua maior derivada tem ordem 1. Além disso não conseguimos isolar a derivada, por isso ela não é uma EDO separável! Vamos verificar se ela é uma EDO exata!

A primeira coisa que temos que fazer é escrever ela no formato de uma EDO exata:

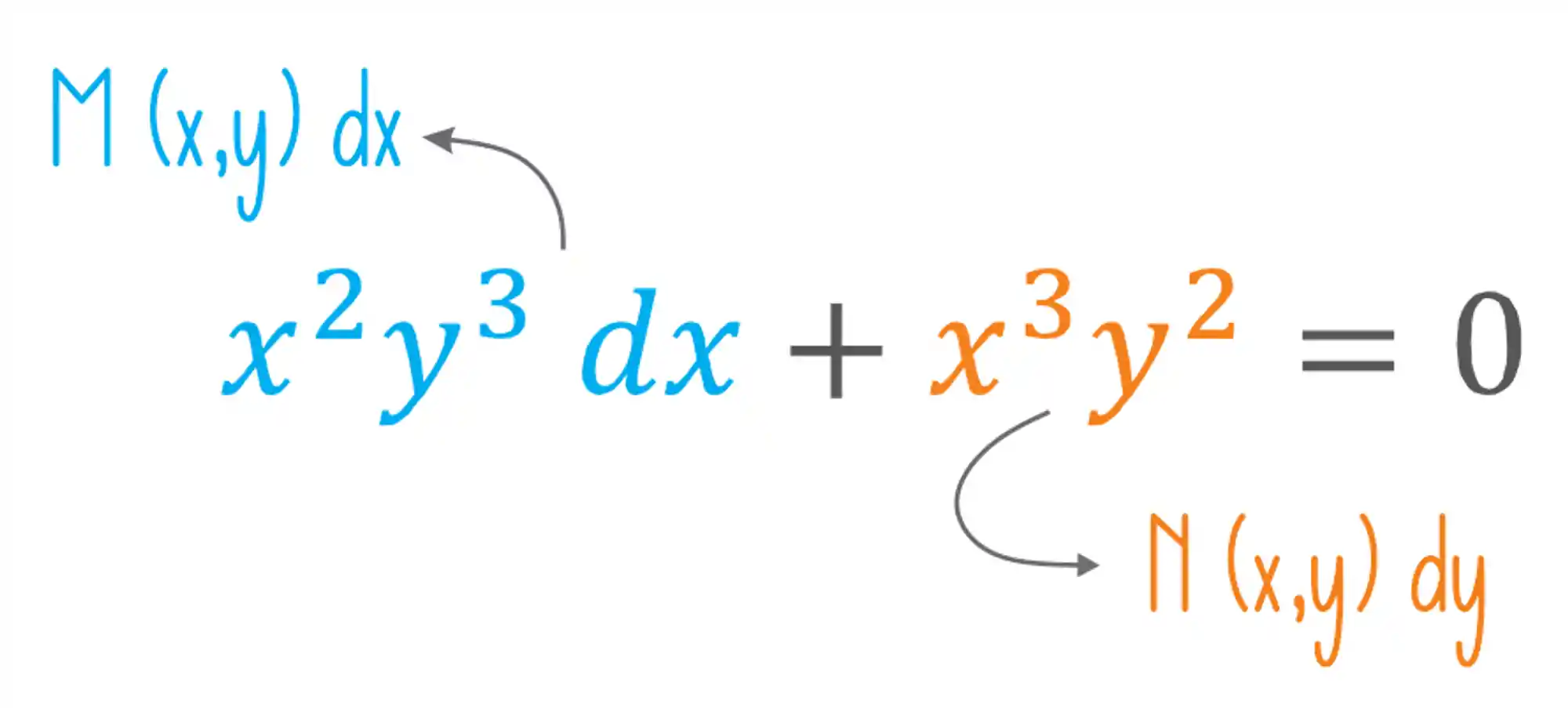
Critério para uma EDO ser Exata
Critério para uma EDO ser Exata

Agora vamos derivar em relação a e em relação a . Se essas duas derivadas forem iguais a nossa equação será exata!

Opaa! Temos uma EDO exata, bora aprender resolve-la?! 😍

📢 Clique para ver mais:

Como Resolver uma EDO de 1ª Ordem Exata

Vamos ver um passo a passo super completinho pra você aprender de uma vez por todas como resolver uma EDO de 1ª ordem exata! Para isso vamos usar o exemplo que vimos a cima:

Passo 1: Confirme que é uma EDO exata

Como vimos ali em cima, uma EDO é exata se obedece os seguintes critérios:

Já fizemos as continhas lá em cima e descobrimos que a nossa EDO é exata! Então podemos pular essa etapa. 😉

Passo 2: Integre em função de

Integrando temos:

Você também pode conferir esse conteúdo em vídeo:

Passo 3: Derive o que foi obtido no passo 2, em relação a y

No passo 2 a gente integrou em relação a . Agora vamos derivar o resultado em relação a , para isso fazemos:

Passo 4: Compare o obtido no passo 3 com N(x)

Comparando o resultado do passo 3 com N(x) a gente consegue isolar g’(x):

Passo 5: Integre g’(x) para achar g(x)

Para isso fazemos:

Passo 6: Obtenha a função 

Agora é só correr pro abraço! 😄 Vamos praticar com mais exercícios?

Exercícios Resolvidos

Exercício Resolvido #1

Exercício nº 1 letra “e” - lista 2 de Cálculo III – IME - UERJ – Profa. Paula Clemente -2014

Resolva a equação diferencial.

d y d x = - x + x y 2 y + x 2 y

Passo 1

Primeira coisa a fazer é ajeitar essa EDO para ver a cara que ela tem, mas da pra ver que separável não deve ser, muito difícil separar isso (se é que é possível)!

Vamos então reescrever a EDO no formato que usamos pras EDOs exatas. Primeiro, multiplicamos cruzado:

y + x 2 y d y = - x + x y 2 d x

E então passamos tudo pro mesmo lado:

x + x y 2 d x + y + x 2 y d y = 0

Opa, ficou com aquela cara bacana pra gente testar se é uma EDO exata!

M x , y = x + x y 2 e N x , y = y + x 2 y

Para ser exata: ∂ M ∂ y = ∂ N ∂ x

∂ M ∂ y = 2 x y

∂ N ∂ x = 2 x y

Logo é uma EDO Exata!!

Passo 2

Integrar M x , y com relação a x

∫ M x , y d x = ∫ ( x + x y 2 ) d x = x 2 2 + x 2 y 2 2 + g ( y )

Passo 3

Derive o obtido no passo 2 com relação a y

∂ x 2 2 + x 2 y 2 2 + g y ∂ y = x 2 y + g ' ( y )

Passo 4

Compare o obtido no passo 3 com N ( x , y )

x 2 y + g ' y = y + x 2 y → g ' y = y

Integrando com relação a y :

g y = y 2 2

Passo 5

Obtenha a função u ( x , y ) inserindo o obtido no passo 4 dentro da função do passo 2  

u x , y = x 2 2 + x 2 y 2 2 + g y = x 2 2 + x 2 y 2 2 + y 2 2

Passo 6

A solução é dada implicitamente por u x , y = c

u ( x , y ) = x 2 + y 2 2 + x 2 y 2 2 = C

Resposta

C = x 2 + y 2 2 + x 2 y 2 2

Exercício Resolvido #2

Exercício nº 1 letra “a” - lista 2 de Cálculo III – IME - UERJ – Profa. Paula Clemente -2014

Resolva a seguinte equação exata:

e y d x + x e y - 2 y d y = 0

Passo 1

Vamos ver se é uma EDO exata!(Mesmo ele dizendo que é, só para treinar)

M x , y = e y e N x , y = x e y - 2 y

Para ser exata: ∂ M ∂ y = ∂ N ∂ x

∂ M ∂ y = e y

∂ N ∂ x = e y

Logo é uma EDO Exata!!

Passo 2

Integrar M x , y com relação a x

∫ M x , y d x = ∫ e y d x = x e y + g ( y )

Passo 3

Derive o obtido no passo 2 com relação a y

∂ x e y + g y ∂ y = x e y + g ' ( y )

Passo 4

Compare o obtido no passo 3 com N ( x , y )

x e y + g ' y = x e y - 2 y → g ' y = - 2 y

Integrando em relação a y temos

g y = - y 2

Passo 5

Obtenha a função u ( x , y ) inserindo o obtido no passo 4 dentro da função do passo 2  

u x , y = x e y + g y = x e y - y 2

Passo 6

A solução é dada implicitamente por u x , y = c

u ( x , y ) = x e y - y 2 = C

Resposta

C = x e y - y 2

Exercício Resolvido #3

Apostila Cálculo 2A –Prof.ª Cristiane R.R. Argento, Prof. Freddy Hernández

Resolva a equação diferencial

( cos ⁡ x cos ⁡ y ) y ' + tg ⁡ x - sen ⁡ x sen ⁡ y = 0

Passo 1

Primeiro a gente precisa saber que tipo de equação é essa. Com essa aí temos que manipular um pouco pra ver que ela tem mesmo cara de exata.

( cos ⁡ x cos ⁡ y ) d y d x + tg ⁡ x - sen ⁡ x sen ⁡ y = 0

cos ⁡ x cos ⁡ y d y + tg ⁡ x - sen ⁡ x sen ⁡ y d x = 0

Agora ela já tá com cara de exata, só vou trocar as posições dos diferenciais para não nos confundirmos depois.

tg ⁡ x - sen ⁡ x sen ⁡ y d x + cos ⁡ x cos ⁡ y d y = 0

Agora já estamos prontos pra resolver a equação. Ou melhor a equação já está pronta pra ser resolvida huauha.

Verificando se ela é exata!

Dada tg ⁡ x - sen ⁡ x sen ⁡ y d x + cos ⁡ x cos ⁡ y d y = 0 é só olhar e ver que M x ,   y = tg ⁡ x - sen ⁡ x sen ⁡ y e que N x , y = cos ⁡ x cos ⁡ y . Logo

∂ M ∂ y = - sen ⁡ x cos ⁡ y = ∂ N ∂ x

Concluímos então que a equação é exata.

Passo 2

Integrando M em relação à x

∫ tg ⁡ x - sen ⁡ x sen ⁡ y d x = - ln ⁡ cos ⁡ x + sen ⁡ y cos ⁡ x + g ( y )

Lembrando que:

ln ⁡ sec ⁡ x = ln ⁡ 1 cos ⁡ x = - ln ⁡ cos ⁡ x

Passo 3

Derive o obtido no passo 2 com relação a y

∂ - ln ⁡ cos ⁡ x + sen ⁡ y cos ⁡ x + g ( y ) ∂ y = cos ⁡ y cos ⁡ x + g ' ( y )

Passo 4

Compare o obtido no passo 3 com N ( x , y )

cos ⁡ y cos ⁡ x + g ' y = cos ⁡ x cos ⁡ y → g ' y = 0 ∴ g y = 0

Passo 5

Obtenha a função u ( x , y ) inserindo o obtido no passo 4 dentro da função do passo 2

u x , y = - ln ⁡ cos ⁡ x + sen ⁡ y cos ⁡ x + g y = - ln ⁡ cos ⁡ x + sen ⁡ y cos ⁡ x

Passo 6

A solução é dada implicitamente por u x , y = c

u = - ln ⁡ cos ⁡ x + sen ⁡ y cos ⁡ x = C

Resposta

As soluções da EDO são dadas implicitamente pela equação

- ln ⁡ cos ⁡ x + sen ⁡ y cos ⁡ x = C

Exercício Resolvido #4

PUC-RJ, Cálculo 3, P1 2014.1, Questão 1 item b

Resolva o problema de valor inicial abaixo, isto é, encontre a função ou as funções y x que satisfaz(em) a equação diferencial e a condição inicial dadas.

2 y 2 x - 3 d x + 2 y x 2 + 4 d y = 0

y 1 = 1

Passo 1

Essa equação tem muito cara de ser exata, mas precisamos verificar isso antes de utilizar o método para resolver EDO’s exatas.

Para isso vamos usar o critério de Euler sabendo que M x , y = 2 y 2 x - 3 e N x , y = 2 y x 2 + 4 . A função M é sempre a que multiplica d x e a função N é sempre a que multiplica d y .

∂ M ∂ y = 4 y x

∂ N ∂ x = 4 y x

Como ∂ M ∂ y = ∂ N ∂ x ela é exata e podemos partir pro abraço porque o método é tranquilo né?

Passo 2

Integrando M x , y em relação a x

∫ 2 y 2 x - 3   d x = 2 y 2 x 2 2 - 3 x + g y = y 2 x 2 - 3 x + g ( y )

Passo 3

Derive o obtido no passo 2 com relação a y

∂ y 2 x 2 - 3 x + g ( y ) ∂ y = 2 y x 2 + g ' ( y )

Passo 4

Compare o obtido no passo 3 com N ( x , y )

2 y x 2 + g ' y = 2 y x 2 + 4 → g ' y = 4 ∴ g y = 4 y

Passo 5

Obtenha a função u ( x , y ) inserindo o obtido no passo 4 dentro da função do passo 2

u x , y = y 2 x 2 - 3 x + 4 y

Passo 6

Como u ( x , y ) = C , onde C é uma constante.

y 2 x 2 - 3 x + 4 y = C

Passo 7

Utilizando as informações do PVI, y 1 = 1 , temos.

y = 1

x = 1

1 2 1 2 - 3.1 + 4.1 = C

C = 2

Passo 8

A solução é dada implicitamente pela equação

y 2 x 2 - 3 x + 4 y = 2

y 2 x 2 + 4 y - 3 x - 2 = 0

Precisamos resolver essa equação para achar y , se liga que ela é uma equação de 2 º grau onde

a = x 2

b = 4

c = - 3 x - 2

Então podemos resolver

y = - 4 ± 4 2 - 4 x 2 - 3 x - 2 2 x 2

y = - 4 ± 16 + 12 x 3 + 8 x 2 2 x 2

y = - 4 ± 4 4 + 2 x 2 + 3 x 3 2 x 2 = - 4 ± 2 4 + 2 x 2 + 3 x 3 2 x 2 = - 2 ± 4 + 2 x 2 + 3 x 3 x 2

Passo 9

Temos que ver qual dos dois sinais que queremos, para isso é só usar a condição inicial, vamos ver o valor de y quando x = 1

y = - 2 ± 4 + 2 . 1 2 + 3 . 1 3 1 2 = - 2 ± 4 + 2 + 3 1 = - 2 ± 9 1 = - 2 ± 3 1

Como o valor de y = 1 neste ponto, a nossa função tem sinal positivo.

y = - 2 + 4 + 2 x 2 + 3 x 3 x 2

Resposta

y = - 2 + 4 + 2 x 2 + 3 x 3 x 2

Exercícios de Livros Relacionados

Em cada um dos problemas 13 e 14, resolva o problema de valor inicial dado e determine, pelo menos aproximadamente, onde a solução é válida 2 x - y + 2 y - x y ' = 0 , y 1 = 3
Verifique se a forma diferencial dada é exata. Justifique. f ) e x 2 + y 2 xd x + yd y
Verifique se a forma diferencial dada é exata. Justifique. i )- y x 2 + y 2d x + x x 2 + y 2 d y ,x , y ∈ Ω , onde Ω é o conjunto x , y ∈ R 2 y0 ∪ { x , y ∈ R 2 | x0 }
Mostre que existem naturais men para os quais a forma diferencial 3 x m + 1 y n + 1 d x + 2 x m + 2 y nd y É exata.
Verifique se a forma diferencial dada é exata. Justifique. d )( x + y )d x + ( x - y ) d y