Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

EDO de segunda ordem: Homogênea

Ver Todos os Exercícios

Teoria

Faaaala aí! Bora aprender sobre EDO de segunda ordem homogêneas com o RespondeAí?!

Então bora lá! Pra começarmos eu vou te mostrar alguns exemplos:

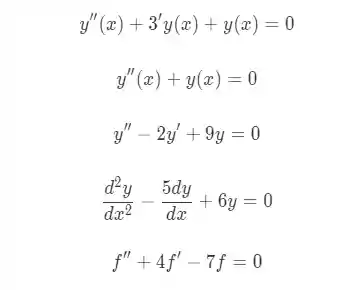
exemplos de EDO homogênea de segunda ordem.
exemplos de EDO homogênea de segunda ordem.

Percebeu alguma semelhança entre elas?

São todas derivadas segundas, por isso equação diferencial ordinária de segunda ordem, ou para os íntimos EDO de segunda ordem! 😆

Mas tem mais! Todas estão igualadas a ZERO e os coeficientes que acompanham as funções e suas derivadas são NÚMEROS. Isso caracteriza nossa EDO homogênea de segunda ordem com coeficientes constantes :)

A forma geral da nossa EDO vai ser assim:

Onde ,  e  são números reais.

Exemplo:

Beleza... Como resolvemos? Vamos começar com esse exemplo aqui

Pra ficar mais fácil, vamos tentar pensar numa função que não mude tanto quando a gente calcula suas derivadas.

Como a gente tem coeficientes constantes, as derivadas estão associadas com a função original por constantes. Então as derivadas são muito parecidas com a função original! 💡💡💡

-Beleza, mas em que que isso ajuda?

É só a gente pensar em uma função cuja derivada é parecidíssima com ela mesma!

Pensou?

São as funções exponenciais! 🤯🤯

Então vamos supor que a solução seja , onde esse vai ser uma constante por enquanto desconhecida.

Vamos então substituir na EDO homogênea:

²

Olha... Tá ficando bem melhor, hein!

Agora, percebe o seguinte: temos o produto de duas parcelas dando zero.

Isso significa que ou uma parcela é zero, ou a outra. Porém, a exponencial nunca é zero! Logo:

Como temos esses dois valores para , vamos fazer uma combinação das possíveis soluções, ficando com:

MUITO MASSA NÉ?

Olha só a generalização: Se tivermos uma EDO desse tipo:

Vamos encontrar a seguinte equação auxiliar:

E depois que descobrirmos o , encontramos o . Observa que a gente tinha uma equação do segundo grau e, no nosso caso, tivemos duas raízes distintas porque nosso famoso delta era positivo... E se não fosse? Bora ver o que acontece!

Casos do discriminante (delta)

Sabendo que tendo a equação:

As raízes são obtidas através de:

E o discriminante é dado por:

Caso Δ>0

Teremos então duas raízes reais e distintas .

Esse foi o caso do nosso exemplo, lembra?

Caso Δ=0

Teremos duas raízes reais e iguais .

Perceba que nesse caso, as exponenciais são iguais, mas a gente multiplica um dos termos pela variável  para que os termos não fiquem iguais! Olha um exemplo:

Montando a equação auxiliar:

Verificando delta:

Encontrando solução geral

Caso Δ<0

Teremos duas raízes complexas :

Mais feio esse aqui né? Liga não, é assim mesmo! Olha um exemplo:

Encontrando a equação auxiliar:

Verificando delta:

Então se liga:

Ignoramos aquele do número com o , basta pegar o valor multiplicado por  para ser o nosso . Assim, encontrando solução geral!

Prontinho! Agora bora praticar com exercícios?! 😆

Casos do discriminante (delta)

Exercícios Resolvidos

Exercício Resolvido #1

EDO de 2ª ordem homogênea

Determine a solução geral y ( x ) da equação diferencial de segunda ordem

y ' ' + y = 0

Passo 1

Colocar a EDO na forma a y ' ' + b y ' + c y = 0 :

y ' ' + y = 0

Legal! A equação já está na forma que queremos!

Passo 2

Encontrar a , b e c :

Comparando as equações:

a y ' ' + b y ' + c y = 0 1 y ' ' + 0 y ' + 1 y = 0

Logo:

a = 1 b = 0 c = 1

Passo 3

Verificar discriminante: Δ > 0 , Δ = 0 ou Δ < 0 ?

Δ = b 2 - 4 a c

Δ = 0 2 - 4 1 ( 1 )

⇒ Δ = - 4

⇒ Δ < 0

Passo 4

Encontrar raízes da equação auxiliar:

a r 2 + b r + c = 0

1 r 2 + 0 r + 1 = 0

⇒ r 2 + 1 = 0

Cálculo das raízes:

r 2 = - 1

⇒ r = ± i

Logo:

r = 0 ± 1 i

Comparando com

r = α ± β i

Temos que

α = 0 β = 1

Passo 5

Encontrar a solução:

y x = e α x c 1 cos ⁡ β x + c 2 sen ⁡ β x

⇒ y x = e 0 x c 1 cos ⁡ 1 x + c 2 sen ⁡ 1 x

⇒ y x = c 1 cos ⁡ x + c 2 sen ⁡ x

Resposta

y x = c 1 cos ⁡ x + c 2 sen ⁡ x

Exercício Resolvido #2

Elaboração Própria

Encontre a solução do problema de valor inicial abaixo:

y ' ' t - 6 y ' t + 8 y t = 0 y 0 = 0 y ' 0 = 2

Passo 1

Colocar a EDO na forma a y ' ' + b y ' + c y = 0 :

y ' ' t - 6 y ' t + 8 y t = 0

Legal! A equação já está na forma que queremos!

Passo 2

Encontrar a , b e c :

Comparando as equações:

a y ' ' ( t ) + b y ' t + c y t = 0 1 y ' ' ( t ) - 6 y ' ( t ) + 8 y ( t ) = 0

Logo:

a = 1 b = - 6 c = 8

Passo 3

Verificar discriminante: Δ > 0 , Δ = 0 ou Δ < 0 ?

Δ = b 2 - 4 a c

Δ = - 6 2 - 4 1 ( 8 )

⇒ Δ = 4

⇒ Δ > 0

Passo 4

Encontrar raízes da equação auxiliar:

a r 2 + b r + c = 0

1 r 2 - 6 r + 8 = 0

⇒ r 2 - 6 r + 8 = 0

Cálculo das raízes:

r = - b ± Δ 2 a = - ( - 6 ) ± 4 2 ( 1 )

⇒ r 1 = 4 r 2 = 2

Passo 5

Encontrar a solução:

y t = c 1 e r 1 t + c 2 e r 2 t

Substituindo os valores de r :

y t = c 1 e 4 t + c 2 e 2 t

⇒ y t = c 1 e 4 t + c 2 e 2 t

Passo 6

Resolver o PVI:

Calcular derivada:

y ' t = 4 c 1 e 4 t + 2 c 2 e 2 t

Substituir t = 0 :

y 0 = c 1 e 4   ⋅ 0 + c 2 e 2 ⋅ 0

⇒ y 0 = c 1 + c 2

y ' 0 = 4 c 1 e 4 ⋅ 0 + 2 c 2 e 2 ⋅ 0

⇒ y ' 0 = 4 c 1 + 2 c 2

Substituir valores iniciais fornecidos:

y 0 = c 1 + c 2 = 0

y ' 0 = 4 c 1 + 2 c 2 = 2

Encontrar as constantes:

c 1 + c 2 = 0 4 c 1 + 2 c 2 = 2

Logo:

c 1 = 1 c 2 = - 1

Substituir constantes na solução geral:

y t = 1 e 4 t + - 1 e 2 t

⇒ y t = e 4 t - e 2 t

Resposta

y t = e 4 t - e 2 t

Exercício Resolvido #3

EDO de 2ª Ordem Homogênea

Seja a equação diferencial E   : y ' ' - 6 y ' + 9 y = 0 . Qual das seguintes afirmações é verdadeira?

(a) A função y t = e 3 t - t e 3 t é a única solução de ( E ) verificando y 0 = 1 e y ' 0 = 2 .

(b) O real 3 é raiz simples da equação característica associada.

(c) A função y t = e - 3 t + 5 t e 3 t é uma solução de ( E ) verificando y 0 = 1 e y ' 0 = 2 .

(d) A função y t = t ( e t + e 3 t ) é solução de ( E ) .

(e) Nenhuma das outras alternativas.

Passo 1

Dando uma olhada nas alternativas, parece que o melhor jeito de proceder é resolver a EDO mesmo (nem sempre é o caso!). Então partiu!

( E ) já está na forma a y ' ' + b y ' + c y = 0 com a = 1 , b = - 6 e c = 9 .

Então o discriminante é:

Δ = b 2 - 4 a c = 36 - 4.1 . 9 = 0

E a equação auxiliar:

r 2 - 6 r + 9 = 0

⇒ r = 6 ± 0 2 = 3

Como Δ = 0 , a solução é da forma

y t = c 1 e r t + c 2 t e r t = c 1 e 3 t + c 2 t e 3 t

Passo 2

Beleza, agora vamos testar as alternativas uma por uma:

Alternativa (a):

Ela dá a função y t = e 3 t - t e 3 t . Podemos ver que ela se encaixa na forma que a gente achou:

c 1 e 3 t + c 2 t e 3 t ⇔ e 3 t - t e 3 t

c 1 = 1     e     c 2 = - 1

Ou seja, essa y é solução da EDO.

Agora resta saber se essa é a única solução respeitando as condições y 0 = 1 e y ' 0 = 2 .

y 0 = 1   ⇒   c 1 e 0 + c 2 . 0 . e 0 = 1   ⇒ c 1 = 1

Vamos calcular a derivada da solução que achamos:

y t = c 1 e 3 t + c 2 t e 3 t

⇒ y ' t = 3 c 1 e 3 t + c 2 e 3 t + 3 c 2 t e 3 t

Ou seja:

y ' 0 = 2   ⇒ 3 c 1 + c 2 + 0 = 2

E como c 1 = 1 :

3 + c 2 = 2

⇒ c 2 = - 1

Concluímos que a função y ( t ) dada pela alternativa (a) realmente é a única solução da EDO verificando y 0 = 1 e y ' 0 = 2 . Portanto a alternativa é verdadeira.

Passo 3

Alternativa (b):

Ela diz: “O real 3 é raiz simples da equação característica associada.”

A equação característica é

r 2 - 6 r + 9 = 0   ⇔ r - 3 r - 3 = 0

Podemos ver que 3 é uma raiz dupla, e não simples, da equação, portanto a alternativa é falsa.

Passo 4

Alternativa (c):

Vimos no passo 2 que a única função solução da EDO verificando verificando y 0 = 1 e y ' 0 = 2 é a da alternativa (a). Portanto essa alternativa é falsa.

Passo 5

Alternativa (d):

Ela afirma que “a função y t = t ( e t + e 3 t ) é solução de ( E ) ”. Nós achamos a forma geral de solução da EDO, que é

y ( t ) = c 1 e 3 t + c 2 t e 3 t

A função não se encaixa na forma que achamos (tem um termo e t ), então a alternativa (d) é falsa.

E a alternativa (e) também está errada porque vimos que a (a) está certa.

Resposta

Alternativa (a)

Exercício Resolvido #4

EDO de 2ª Ordem homogênea

Considere a equação diferencial y ' ' + p x y ' + q x y = 0 , com p x e q x funções reais.

Sabendo que y 1 x = e x e y 2 x = x 2 são soluções da equação, determine p x e q x .

Passo 1

Para acharmos p x e q x vamos substituir as duas soluções da EDO e ver o que temos, começando com y 1 x = e x

y 1 = e x

y 1 ' = e x

y 1 ' ' = e x

Substituindo na equação vamos ter

e x + p x . e x + q x . e x = 0

Colocando e x em evidência

e x 1 + p x + q x = 0

Como e x é sempre diferente de 0 , vamos ter

1 + p x + q x = 0

Passo 2

Vamos agora substituir os valores de y 2 x = x 2

y 2 = x 2

y 2 ' = 2 x

y 2 ' ' = 2

Substituindo na equação vamos ter

2 + p x . 2 x + q x . x 2 = 0

2 + 2 x p x + x 2 q x = 0

Passo 3

Vamos ter o seguinte sistema

1 + p x + q x = 0 2 + 2 x p x + x 2 q x = 0

Multiplicando a primeira equação por - x 2 vamos ter

- x 2 - x 2 p x - x 2 q x = 0

Somando com a segunda equação, vamos ter

2 - x 2 + 2 x p x - x 2 p x = 0

p x 2 x - x 2 = x 2 - 2

p x = x 2 - 2 2 x - x 2

Substituindo esse valor na primeira equação vamos ter

1 + x 2 - 2 2 x - x 2 + q x = 0

q x = - x 2 + 2 2 x - x 2 - 1

Igualando os denominadores, vamos ter

q x = - x 2 + 2 - 2 x + x 2 2 x - x 2

q x = 2 - 2 x 2 x - x 2

Resposta

p x = x 2 - 2 2 x - x 2

q x = 2 - 2 x 2 x - x 2

Exercícios de Livros Relacionados

Calcule a e b:f ) ((i + 1)^2)/((i - 1)^2) = a + b i
Considere o problema de valor inicial 2 y ' ' + 3 y ' - 2 y = 0 , y 0 = 1 , y ' 0 = - α , em que α0 .Resolva o problema de valor inicial.Faça o gráfico da solução em α = 1 . Encontre as coordenadas t
Resolva a equação diferencial.2 (d^2 y)/(d t^2) + 2 (2 d y)/(d t) - y = 0
Resolva o problema de contorno, se possível.y^(' ') + 2 y^' = 0 , y (0) = 1 , y (1) = 2