Máximos e Mínimos Globais numa Região Aberta
Produzido por Bruno NeresTeoria
Olá, pessoal! Tudo bom? Então, o nosso papo aqui é sobre máximo e mínimo globais. Vamos lá!
Quando nós temos uma região fechada, os nossos primeiros passos para encontrar um máximo e mínimo global são: achar os pontos críticos da função e depois verificar quais que estão dentro da região fechada ou na fronteira.
Mas se eu tenho uma região aberta? Como eu vou saber quais pontos críticos considerar? Então, nesse caso a gente vai considerar TODOS os pontos críticos da função.
Parece trabalhoso, né? Mas relaxa, que é mais simples do que você imagina. Vem comigo e vamos resolver o exemplo abaixo,
A gente quer saber qual é o máximo ou mínimo global dessa função. Vamos de um passo a passo então
Passo 1: Achar o ponto crítico
Para isso, nós tem que achar o nosso e igualar a zero. E a gente faz isso derivando,
O único ponto crítico é , ou seja, é o único ponto onde o nosso vai zerar. Como ele é o único ponto, se houver máximo ou mínimo global de ele ocorrerá nesse ponto.
Passo 2: Descobrir se esse ponto é um máximo ou mínimo global
A gente começa substituindo o nosso ponto crítico na função,
Pronto, vimos que a função zera nesse ponto, mas agora a gente precisa mostrar que esse é um ponto de máximo ou mínimo!
Então, galerinha, para fazer isso, eu vou dar uma mexidinha nela, pois assim a gente vai enteder melhor como ela funciona!
Repara que a nossa função é a soma de dois termos que estão ao quadrado, ou seja, ela é sempre positiva. Em outras palavras,
Opa, lembra que nosso deu zero! Então significa que ele é um ponto de mínimo, pois a nossa função é sempre maior que zero. Mas agora nós temos que mostrar que ele é mínimo global. Ou seja, mostrar que .
Repara que a gente já fez isso quando vimos que a função é uma soma de termos ao quadrado. Olha aqui:
Como,
E,
Logo, para todo . Portanto é ponto de mínimo global.
Vamos dar uma olhada no gráfico da função,
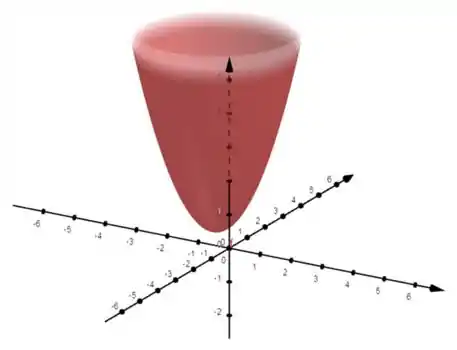
Aqui no gráfico a gente consegue ver esse mínino, mas repara que a gente não precisou desenhá-lo para achar o nosso ponto crítico.
Resumindo...
Quando quisermos descobrir qual o máximo e mínimo de uma região aberta, vamos seguir dois passos:
- Encontrar o ponto crítico da função,
- Mostrar que ele é um máximo ou mínimo global:
- Para máximo global mostrar que .
- Para mínimo global mostrar que .
Para gente ficar craque nisso precisamos treinar com outras funções. Então, partiu exercícios!