Máximos e Mínimos Globais numa Região Fechada
Produzido por Bruno NeresTeoria
Qual a ideia principal?
Podemos achar os máximos e mínimos de uma função em todo o domínio dela, mas também em uma região fechada.
Para isso, só vamos considerar os pontos críticos dentro dela. Além disso, também vamos ter que testar a fronteira da região.
Por que isso é importante?
Porque numa região fechada, nem sempre os máximos e mínimos globais vão ser em pontos críticos! Eles podem ocorrer também na fronteira da região!
Tem uma diferença interessante nesse tipo: as vezes ao olhar o domínio todo uma função pode não ter máximo ou mínimo global. Mas, quando analisamos uma região fechada, isso não vai ocorrer!
Exemplo Prático
A função não tem máximo global: podemos aumentar o valor de o quanto quisermos aumentando e .
Agora, se fizermos uma restrição, por exemplo, o retângulo a história já muda! Nessa região tem um máximo global: quando e , e o valor desse máximo é . Deu pra captar?
Beleza, e geralmente, pra facilitar nossa vida, a região fechada na qual trabalhamos é um retângulo, onde temos e limitados por duas constantes.
No exemplo que eu mencionei lá em cima nosso retângulo é:
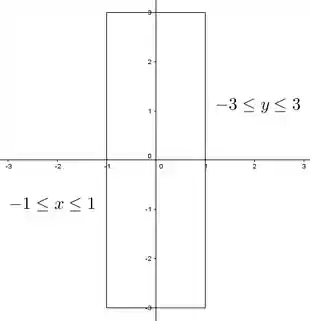
A vantagem disso é que as fronteiras de um retângulo são fáceis de analisar, são retas!
Repare que em cada lado do retângulo uma das coordenadas ( ou ) é fixa, enquanto a outra varia. Ou seja, mesmo uma função sendo de 2 variáveis, nos lados de um retângulo como esse ela só depende de uma!
É como se tivéssemos 4 funções de 1 variável (uma pra cada lado). E aí vamos ter que achar os pontos críticos dessas “subfunções”, derivando e igualando a zero.
Todos os pontos críticos achados nos 4 lados também serão candidatos a ponto de máximo ou mínimo da função no retângulo.
Enfim, vejamos um exemplo que vai ser mais fácil de explicar na prática. Vamos determinar o máximo e o mínimo globais da função
na região delimitada por e .
Fazendo o passo a passo para obter os pontos críticos a gente vai encontrar esse aqui
Repare que esse ponto pertence à nossa região, pois ele satisfaz e . Então vamos guardar ele.
Agora temos que testar a fronteira! Quando temos um retângulo (no caso, é até um quadrado), a primeira coisa que temos que fazer é separar os vértices do retângulo. Eles automaticamente já são candidatos a ponto de máximo ou mínimo. Então não se esqueça deles! :)
Nesse caso, temos os pontos
Então entraram mais 4 pontos pra nossa lista.
Agora sim, vamos ver de fato as fronteiras, que nada mais são que os lados do nosso quadrado.
Vou nomear esses lados de lado 1, 2, 3 e 4, da seguinte forma:
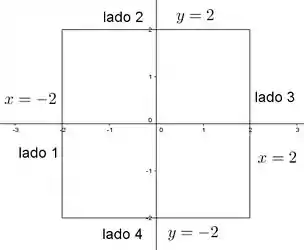
Vamos começar pelo lado 1. Nele temos
Como é fixo, nesse lado a função só depende de !
Agora derivamos essa função (derivada normal de uma função de 1 variável):
E igualamos a derivada a zero, pra achar os pontos críticos:
Então nesse lado só temos um ponto crítico! O é fixo, vale , e achamos , então esse ponto é .
Agora vamos fazer a mesma coisa pros outros lados!
No lado 2, temos
Então agora a função só depende de , já que o é fixo:
Derivando e igualando a zero:
Portanto, no lado 2 temos mais um candidato: o ponto .
No lado 3:
Então
Derivando e igualando a zero:
Então achamos mais um ponto: .
Vamos pro último lado, o lado 4:
Temos
Logo,
Ufa, achamos nosso último ponto! O ponto .
Estamos quase acabando! Resumindo, nossos candidatos a ponto de máximo e mínimo de no retângulo são o ponto crítico de , os 4 vértices do retângulo, mais os 4 pontos que achamos nos lados do retângulo:
, , , , , , , e
Passo Final: Avaliar a Função em Todos os Pontos
Agora temos que calcular o valor da função em todos esses pontos: o menor será o mínimo global e o maior o máximo global.

O menor valor é logo no primeiro ponto e o maior ficou no terceiro ponto.
Portanto os pontos e são, respectivamente, os pontos de mínimo global e máximo global de dentro do retângulo .
O valor mínimo é , enquanto o valor máximo é .
Essas questões não costumam ser difíceis, mas são chatinhas pelo grande número de contas, e por serem muito repetitivas.
Resumindo:
O passo a passo é:
- Achar pontos críticos da função
- Determinar quais estão na região fechada
- Guardar os que estiverem nela, descartar os que não estiverem
- Guardar vértices da região
- Achar candidatos a máximo e mínimo na fronteira, lado por lado
- Calcular o valor da função em todos os pontos achados
- Determinar qual é o máximo global e qual é o mínimo global
Agora é praticar pra ficar craque nisso! :)
Passo Final: Avaliar a Função em Todos os Pontos
Resumindo:
Exercícios Resolvidos
Exercício Resolvido #1
Cálculo 2 UERJ, Lista 4 Prof. Hamilton, exercício 8b
Encontre os pontos de máximo e mínimo globais da função dentro de .
Passo 1
Para encontrar os pontos de máximo e mínimo globais de uma função com restrição o processo é sempre o mesmo: Verificar se há um ponto crítico dentro da região, e verificar se há máximos e mínimos na fronteira da região.
Verificando pontos críticos dentro da região:
Assim,
Passo 2
Como nos pontos críticos , então
Logo, temos 4 pontos críticos, que são as combinações dos e que encontramos. São eles:
Os pontos e já podem ser descartados, já que eles ficam fora da região que estamos considerando ().
Passo 3
Então guardamos os pontos e . Também precisamos guardar os vértices do retângulo que é a nossa região.
São os pontos:
Portanto, temos mais 4 pontos candidatos a máximo e mínimo.
Passo 4
Agora, devemos verificar pontos de máximo ou mínimo na fronteira.
Assim, temos 4 lados a serem verificados:
Quando em que são os lados do retângulo.
Em cada lado a função só depende de uma variável, e nós temos que achar os pontos críticos dessas 4 “subfunções”.
Passo 5
Comecemos pelo lado . Lembrando a nossa função:
E o primeiro lado:
Substituindo o lado na função:
Temos que achar o valor de máximo dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a
Então temos pontos críticos em
E
Passo 6
Agora precisamos fazer o mesmo pro segundo lado :
Substituindo esse lado na função, teremos:
Desenvolvendo,
Temos que achar os pontos críticos dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a
Então temos os pontos
E
Mas já vimos antes esses dois pontos como pontos críticos de , então o lado 2 não acrescentou nada de novo!
Passo 7
Vamos verificar para o terceiro lado :
Substituindo-o na função:
Desenvolvendo,
Neste caso derivamos em relação a
(lembrando que .
Assim, obtemos o ponto . Mas ele nós já consideramos, é um vértice do retângulo!
Então o lado 3 também não acrescentou nada novo.
Passo 8
Finalmente!! Esse é o último lado! Aguente firme!!! Não tem nada de especial nele... só repetir o mesmo processo que fizemos até agora.
Quarto lado:
Substituindo-o na função:
Desenvolvendo,
Temos que achar os pontos críticos, vamos derivar e igualar a zero. Neste caso derivamos em relação a
E vamos ter o ponto , que também já achamos!
Passo 9
Ok, agora já temos todo o material necessário para terminar de vez com isso e dizer quais são os pontos de máximo e mínimo!
Os nossos candidatos são os pontos:
Passo 10
Só nos resta calcular o valor da função em cada ponto. Lembrando que
Então temos
Show, então os ponto de mínimo global e máximo global de são, respectivamente, e .
O valor mínimo é e o valor máximo é .
Resposta
Exercício Resolvido #2
Cálculo 2 UNICAMP, Exame 2014 Tarde, questão 2
Determine os valores máximo e mínimo absolutos de
no conjunto
Passo 1
Antes de mais nada, é bom visualizar o conjunto . E nesse caso, até que é bem simples: temos e . Então e . vai ser um quadrado:
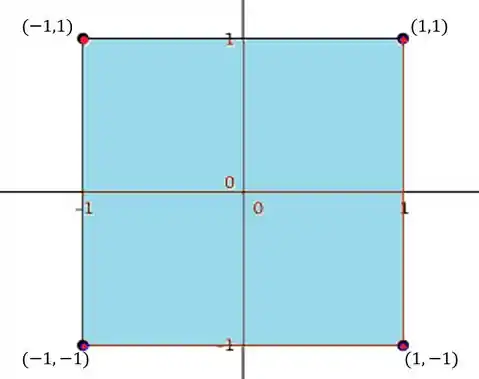
Dito isso, podemos continuar :)
Passo 2
Essa é uma questão de máximos e mínimos, então o nosso primeiro reflexo tem que ser: achar as derivadas parciais de e igualá-las a para achar os pontos críticos de . Então vamos lá:
Logo:
Agora igualando a :
- Se , como então ; o que nos dá o ponto .
- Se então ; o que nos dá os pontos .
Mas repare que esses dois últimos pontos não pertencem ao quadrado . Logo, o único ponto crítico de em é .
Passo 3
Agora vamos dar uma olhada na fronteira do quadrado. Podemos notar que os vértices do quadrado são candidatos a máximo e mínimo, pois eles são os extremos da região. Isso nos dá mais 4 candidatos: os pontos , , e .
Vamos analisar agora os lados do quadrado um por um. Repare que vamos sempre ter uma coordenada variando de -1 a 1 enquanto outra fica fixada. Ou seja, na borda do quadrado a só depende de uma variável.
Por isso, pra facilitar nossa conta, vamos criar uma função de uma variável para cada lado e determinar os pontos críticos dessas funções. Esses pontos críticos também vão ser candidatos a máximo ou mínimo da no quadrado. Ficou confuso? Relaxa que não é tão complicado, dá uma olhada:
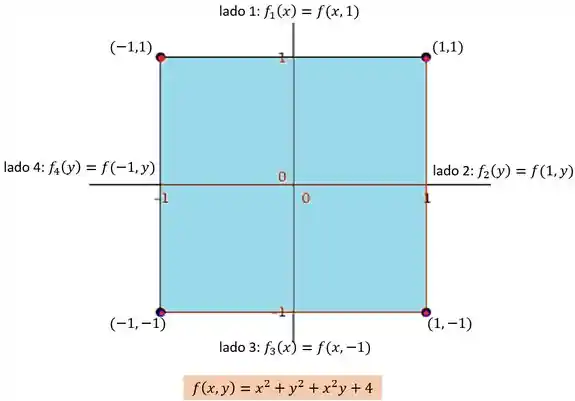
Passo 4
Lado 1: e
tem um ponto crítico: o ponto , que é, portanto, mais um candidato a ponto de máximo ou mínimo.
Lado 2: e
Assim, obtemos mais um candidato, o ponto .
Lado 3: e
A função é consante então para todo vamos ter .
Então, o lado 3 todo é candidato a conter o valor máximo ou mínimo de no quadrado. Já tínhamos considerado como candidatos os vértices e . Mas agora podemos considerar todos os pontos , com , beleza?
Lado 4: e
Repare que . Então, que nem pra , vamos ter que o ponto crítico de tem . Mas agora . Isso nos dá mais um candidato, o ponto .
Passo 5
Show! Achamos todos os candidatos a ponto de máximo ou mínimo de no quadrado, são os pontos:
Agora "só" nos resta calcular o valor da em cada ponto e ver qual vai ser o máximo e qual vai ser o mínimo! Lembrando que , vamos ter:
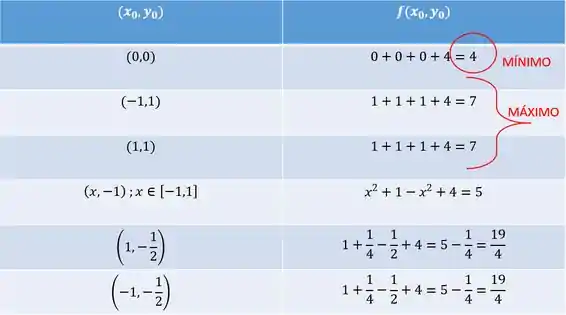
Comparando os valores, podemos ver que o valor mínimo é , no ponto , enquanto o valor máximo é , nos pontos e .
Resposta
Máximo: , nos pontos e
Mínimo: , no ponto .
Exercício Resolvido #3
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, exercício 37 p.357 (modificado)
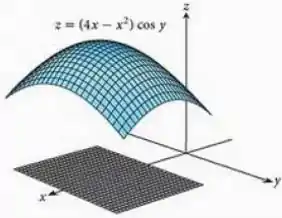
Encontre o máximo e o mínimo absoluto da função
na placa retangular (veja figura a seguir).
Passo 1
Vamos achar os pontos críticos da função, igualando as derivadas parciais a zero:
Temos
Passo 2
Comecemos pela derivada parcial em relação a :
Vamos ver as restrições da placa retangular:
Portanto, sem problemas pra , mas não pode!
Então concluímos que .
Passo 3
Agora zeremos a derivada parcial em relação a :
Se :
Mas como , nenhum dessas opções é válida.
Então nos sobra . Como , devemos ter .
Portanto, possui um ponto crítico nessa placa retangular: o ponto . Ele é o nosso primeiro candidato a ponto de máximo ou mínimo absoluto da função na placa.
Passo 4
Agora temos que analisar a fronteira do retângulo:
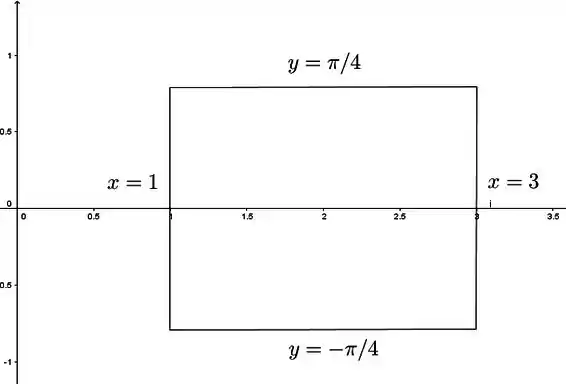
Vamos estudar os lados um por um e determinar que candidatos a ponto de máximo ou mínimo temos em cada um deles.
Passo 5
Os primeiros candidatos que podemos separar são os 4 vértices do retângulo, os pontos:
Agora sim vamos olhar os lados um por um.
Passo 6
Começando pelo lado de cima, onde
Assim, nesse lado a função passa a depender só de :
Derivando e igualando a zero:
Portanto, o ponto é mais um candidato.
Passo 7
Vejamos agora o lado da direita:
Agora a função só depende de :
Continuando:
Então achamos mais um ponto: .
Passo 8
Passamos agora pro lado de baixo:
Nesse lado, temos
Repare que a função ficou igual ao lado de cima. Da mesma forma, temos
Então encontramos mais um ponto: .
Passo 9
Enfim chegamos ao último lado, o da esquerda, onde
Aqui temos
Essa ficou igual ao lado da direita. Assim,
Achamos o último candidato: o ponto .
Passo 10
Agora só nos resta calcular o valor da função em todos esses pontos e determinar qual é o mínimo global e qual é o máximo global:

Portanto, o valor máximo de na placa retangular é , atingido no ponto .
O valor mínimo é , obtido nos pontos e .
Aliás, podemos ver que esses pontos são compatíveis com a figura.
Resposta
Máximo: , em .
Mínimo: , em e .
Exercício Resolvido #4
Cálculo 2 USP, PSUB 2012, questão 4
Sejam número real, e .
(a) Classifique os pontos críticos de em função de .
(b) Considere . Encontre os valores máximo e mínimo de no conjunto
Passo 1
(a)
Questão de pontos críticos não tem erro: basta achar as derivadas parciais, igualá-las a 0 e depois mandar ver no teste da derivada segunda! Então vamos lá, nós temos:
Então as derivadas parciais vão ser:
Passo 2
Agora vamos igualar essas derivadas a zero. Primeiro pra derivada parcial em :
E agora pra derivada parcial em relação a :
já que .
Portanto, os pontos críticos de são e
Passo 3
Vamos começar calculando as derivadas segundas de , pra depois aplicar o teste da derivada segunda:
Logo:
Também temos:
E pras derivadas mistas:
Passo 4
Firmeza! Agora podemos partir pro teste da derivada segunda:
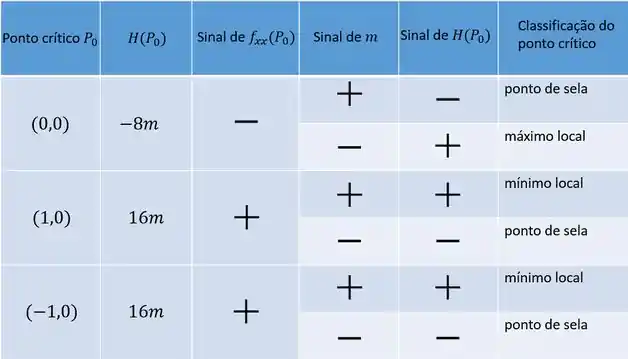
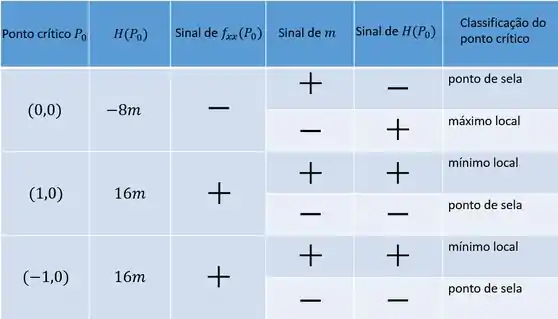
Agora vem a parte delicada, vamos ter que classificar os pontos críticos que achamos em função de :
- Ponto : e
- Ponto : e
- Ponto e
Pra ficar mais claro, podemos classificar os pontos críticos de em função do sinal de em uma tabela:
Passo 5
(b)
Nessa questão então:
Vamos achar todos os candidatos a ponto de máximo ou mínimo de em , ou seja que respeitem as seguintes condições:
Temos que considerar candidatos no interior e na borda do conjunto .
Podemos notar que nenhum dos candidatos que achamos na letra (a) estão no interior de . De fato:
- (borda de )
- (fora de )
- (fora de )
Então todos os nossos candidatos a pontos de máximo e mínimo estão na borda de .
Vamos dividir a borda em 3 partes:
- pontos com e
- pontos com e
- pontos das extremidades: e ou
Vamos ver melhor isso no próximo passo! :)
Passo 6
1. Vamos começar com os pontos de onde e . A vai ficar dependendo de uma só variável, aí vamos poder usar o clássico procedimento de derivar e igualar a derivada a 0 e assim achar os pontos críticos!
A função vai ficar assim:
Primeiro, derivando:
Agora, igualando a derivada a 0:
Temos 2 possibilidades, ou , ou:
E como
Portanto, achamos 3 candidatos: os pontos ; e .
Observação: se deixar também tá bom, eu que sou fresco e gosto de botar :)
Passo 7
2. Vamos agora aos pontos com e . Usando o mesmo procedimento do passo anterior, temos:
Derivando:
Igualando a 0:
Vamos só guardar o caso pois não respeita a condição . Vamos deixar esses daí pro próximo passo :)
Enfim, achamos mais um candidato: o ponto .
Passo 8
3. Agora sim, vamos considerar as extremidades, são os pontos onde .
Portanto, temos mais 2 candidatos: e .
Assim, temos ao todo 6 candidatos:
Passo 9
Próximo passo: calcular o valor da função em cada ponto e determinar qual é o máximo e qual é o mínimo. Partiu? Lembrando que:
Ou seja, ficou assim:
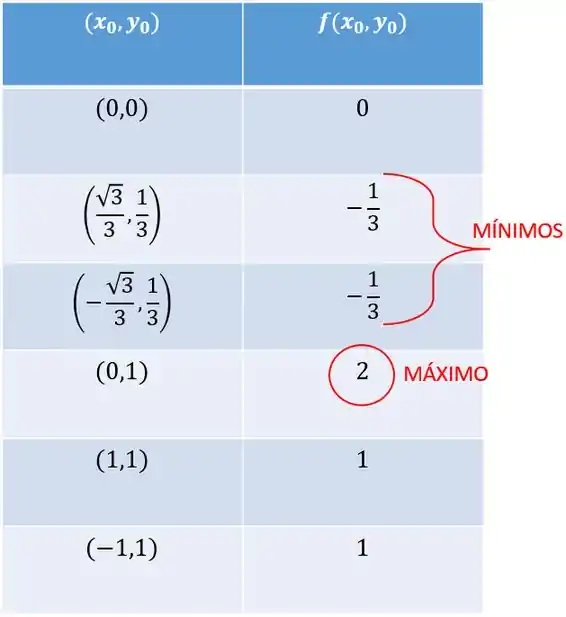
Enfim conseguimos achar os extremantes de no conjunto :
- Os pontos de mínimo são e o valor mínimo é .
- O ponto de máximo é e o valor máximo é .
Resposta
(a)
(b)
Os pontos de mínimo são e o valor mínimo é .
O ponto de máximo é e o valor máximo é .