Substituição Trigonométrica
Produzido por Arthur Melo de AlmeidaTeoria
Bora aprender a fazer Substituição Trigonométrica?!
Então já vamos começar com tudo! Eu quero que vc pense em como você resolveria esse problema aqui:
Difícil, não é? 😱
Calma! Fica comigo que você vai aprender! Vamos resolver essa integral por substituição trigonométrica! 😉
Só que ai você me pergunta
-“ Como você sabia que da pra resolver esse problema com substituição trigonométrica? Eu não to vendo nenhum seno, cosseno, tangente e afins.. 😖”
Excelente questão! Vamos começar entendendo quando usar a substituição trigonométrica para resolver a integral!
Quando usar a Substituição Trigonométrica?
Sempre que alguma parte da nossa integral se parecer com algum desses casos aqui:
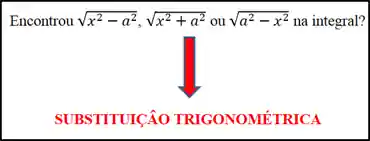
Agora, vamos dar uma olhadinha no nosso exemplo inicial?
Opaa, ali no denominador temos um
Para cada caso, vamos fazer um tipo de substituição:
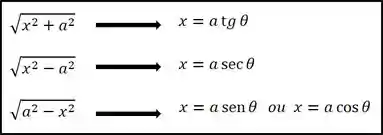
Como Fazer a Integral por Substituição Trigonométrica?
Vamos aprender na prática, resolvendo o nosso exemplo!
Passo 1: Identificar o caso da Substituição Trigonométrica
O primeiro passo a gente meio que já fez! Temos que olhar pra nossa integral, olhar pro quadrinho de casos que se encaixam na substituição trigonométrica e ver onde que ele se encaixa!
Mas recapitulando, temos
Logo, faremos:
Que vai ficar:
Passo 2: Calcular
Já conhecemos o
Então temos que deriva-lo para achar
Pra agilizar as contas e dar aquele confere você pode usar nossa calculadora de derivadas!
Passo 3: Substituir o
Substituindo:
Podemos dar uma arrumadinha nisso, pra te ajudar você pode dar uma conferida na nossa tabela de relações trigonométricas!
Ficamos com:
Bem menos assustador!
Passo 4: Calcular a Integral com relação a
Passo 5: Converter o
Vamos considerar o triângulo retângulo:
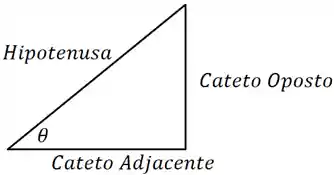
Sabemos que:
Para o nosso exemplo:
Logo:
Só pra a gente visualizar melhor, podemos jogar no triângulo:
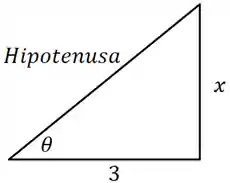
Huuum…acho que rola um teorema de pitágoras aqui:
Agora podemos completar nosso triângulo retângulo:
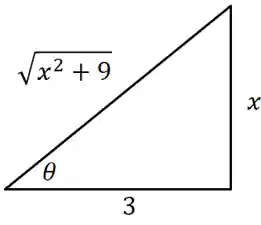
Podemos voltar pro nosso problema…
Podemos reescrever o
Então ficamos com:
Awee!!
Pra conferir essa resposta você também pode usar nossa Calculadora de Integrais! 😉
DESAFIO: Resolva a seguinte Integral usando Substituição Trigonométrica
A resolução desse problema você pode conferir nesse vídeo abaixo:
Bora praticar com mais exercícios?