Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 7.3 - Ex. 2

Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado.

∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ

Passo 1

Eaee, belezinha?? Bom... queremos calcular a seguinte integral:

∫ x 3 9 - x 2 d x

Para isso, devemos utilizar a substituição trigonométrica para resolver ela.

Por sorte a questão nos deu a substituição que deveremos fazer:

x = 3 sin ⁡ θ

Com esse dado, devemos fazer um triângulo retângulo associado e analisar como isso nos va ajudar a resolver a questão.

E aí? Bora lá?? 😉

Passo 2

Com a substituição que nos foi dada, vamos isolar o θ para desenharmos o triângulo:

x = 3 sin ⁡ θ ∴

x 3 = sin ⁡ θ ∴

θ = sin - 1 ⁡ x 3

Com isso, temos o seguinte triângulo retângulo:

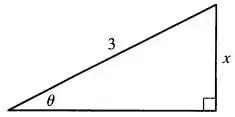
Aplicando o Teorema de Pitágoras, encontramos o outro cateto c :

3 2 = x 2 + c 2 ∴

c = x 2 - 9

Portanto, temos:

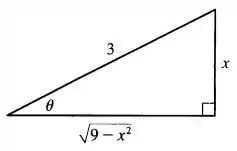
Passo 3

Essas integrais com substituição trigonométricas são um pouco confusas, mas vamos fazer passo a passo com calma que você vai ver que com a prática é possível não se descabelar por isso (ou não rs).

O problema nos dá o seguinte:

x = 3 sin ⁡ θ

Então, diferenciando

d x = 3 cos ⁡ θ d θ

Temos que:

9 - x 2 = 9 - 9 sin 2 ⁡ θ ∴

9 - x 2 = 9 ( 1 - sin 2 ⁡ θ ∴

9 - x 2 = 9 cos 2 ⁡ θ ∴

9 - x 2 = 3 c o s ⁡ ( θ )

Passo 4

Agora, a gente precisa calcular a integral, pra facilitar, vamos fazer a substituição dada

∫ x 3 9 - x 2 d x = ∫ 3 sin ⁡ θ 3 ⋅ 3 cos ⁡ θ ⋅ 3 cos ⁡ θ d θ ∴

∫ x 3 9 - x 2 d x = 3 5 ∫ sin 3 ⁡ θ cos 2 ⁡ θ d θ ∴

∫ x 3 9 - x 2 d x = 3 5 ∫ sin 2 ⁡ ( θ ) cos 2 ⁡ ( θ ) s i n ⁡ ( θ ) d θ

Voce precisa se lembrar da seguinte propriedade trigonométrica: cos 2 ⁡ ( θ ) + sin 2 ⁡ ( θ ) = 1 .

Aí a gente substitui na integral:

∫ x 3 9 - x 2 d x = 3 5 ∫ 1 - cos 2 ⁡ θ cos 2 ⁡ ( θ ) s i n ⁡ ( θ ) d θ

Passo 5

Agora, a gente pode resolver pelo método da substituição:

Seja u = c o s ⁡ ( θ ) , temos que d u = - sin ⁡ θ d θ . Então, substituindo:

∫ x 3 9 - x 2 d x = 3 5 ∫ 1 - u 2 u 2 - d u ∴

∫ x 3 9 - x 2 d x = 3 5 ∫ - u 2 + u 4 d u ∴

∫ x 3 9 - x 2 d x = 3 5 1 5 u 5 - 1 3 u 3

Substituindo u

∫ x 3 9 - x 2 d x = 3 5 1 5 u 5 - 1 3 u 3 + c ∴

∫ x 3 9 - x 2 d x = 3 5 1 5 cos 5 ⁡ θ - 1 3 cos 3 ⁡ θ + c ∴

∫ x 3 9 - x 2 d x = 3 5 1 5 cos 5 ⁡ ( θ ) - 1 3 cos 3 ⁡ ( θ ) + c

Passo 6

Lembra la no começo quando dissemos que cos ⁡ θ = 9 - x 2 / 3 ?! Agora é só a gente substituir:

∫ x 3 9 - x 2 d x = 3 5 1 5 cos 5 ⁡ θ - 1 3 cos 3 ⁡ θ + c ∴

∫ x 3 9 - x 2 d x = 3 5 1 5 9 - x 2 3 5 - 1 3   9 - x 2 3 3 + c ∴

∫ x 3 9 - x 2 d x = 3 5 1 5 9 - x 2 5 2 3 5 - 1 3 9 - x 2 3 2 3 3 + c ∴

∫ x 3 9 - x 2 d x = 1 5 9 - x 2 5 2 - 3 9 - x 2 3 2 + c

Entendeu direitinho?? Responde aee 😉

Resposta

∫ x 3 9 - x 2 d x = 1 5 9 - x 2 5 2 - 3 9 - x 2 3 2 + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 x 2 + 9 d x ; x = 3 tg ⁡ θ
Calcule a integral indefinida: ∫ d t 9 - 16 t 2
Calcule a integral indefinida: ∫ e x e 2 x + 1d x
Calcule a integral indefinida: ∫ x 2 - 1 x 2d x