Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integração por Frações Parciais

Ver Todos os Exercícios

Teoria

Hoje vamos aprender o Método das Frações Parciais para resolver integrais e não sofrer mais!

Imagina, se deparar com uma integral dessa daqui na prova, o que você faz?

Chora? CLARO QUE NÃO! Você vai é resolver ela sem medo e com confiança usando o método das frações parciais que vou te ensinar agora. 🤩🤩🤩

Mas antes de qualquer coisa, vamos aprender quando vamos usar o método de frações parciais ao invés de outro método, como substituição ou integração por partes!

Quando usar Frações Parciais?

O método de integração por frações parciais serve para resolver integrais de frações e polinômios quando o grau do polinômio do denominador é maior que o grau do polinômio do numerador.

Dá uma conferida nesse vídeo abaixo a gente te explica direitinho quando usar frações parciais! 👇

📢 Clique para saber mais:

Como Integrar por Frações Parciais?

O que a gente vai fazer aqui é separar uma fração, que é difícil de integrar, em duas ou mais frações, que são mais simples de integrar! Assim:

Mas antes de aprender como fazer essa “mágica”, precisamos ter em mente esses 4 casos que podem aparecer:

  • Caso 1: Fatores Lineares Distintos
  • Caso 2: Fatores Lineares Repetidos
  • Caso 3: Fatores Quadráticos Distintos
  • Caso 4: Fatores Quadráticos Repetidos

Bora colocar a mão na massa?!

Caso 1: Fatores Lineares Distintos

Aqui a gente vai resolver aquele exemplo lá de cima:

Queremos "quebrar" essa fração em outras frações mais simples:

Agora vamos para o passo a passo!

PASSO 1: Fatorar o denominador da fração.

Como esse denominador é um denominador de segundo grau, para fatorarmos basta encontrarmos as raízes, e , e reescrever ele na forma:

As raízes são e . Reescrevendo temos:

PASSO 2: Reescrever a fração como uma soma de frações

Vamos dizer que a fração complicada que temos será igual a soma de outras frações, nas quais os denominadores são as parcelas que encontramos na fatoração do passo anterior e os numeradores são constantes, ainda desconhecidas. Assim:

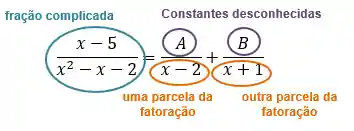
"Quebra" da fração em uma soma de frações

PASSO 3: Encontrar os valores de e

Para isso vamos fazer o MMC na expressão que encontramos no passo anterior. Assim:

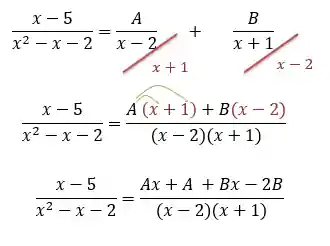
Fazendo o MMC
Fazendo o MMC

Agora, temos que o numerador do lado esquerdo tem que ser igual ao numerador do lado direito:

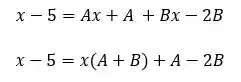
Igualando os numeradores
Igualando os numeradores

Agora, temos que comparar tudo o que tem e tudo o que não tem , assim:

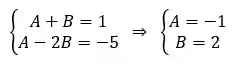
Comparando os numeradores
Comparando os numeradores

E prontinho, temos a nossa fração complicado escrita como uma soma de frações mais simples:

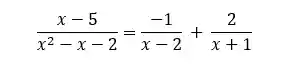
Fração reescrita em frações parciais
Fração reescrita em frações parciais

Agora só integrar essas duas frações:

Prontinho! Agora vamos ver os outros casos!

Caso 2: Fatores Lineares Repetidos

Nesse caso os fatores do denominador são todos do 1º grau e alguns fatores se repetem (aparecem raízes múltiplas), assim:

Fica atento que nem sempre o denominador já vai vir fatorado, e aí a gente vai ter que fatorar. Mas nesse caso já está fatorado, bom pra gente. Dado que polinômio do denominador tem uma raiz única e uma raiz múltipla .

Vamos quebrar dessa forma:

Depois é só conta, trabalho braçal: botar tudo no mesmo denominador, montar e resolver o sistema... Faça essas continhas sempre prestando bastante atenção.

Agora, saca só essa outra aqui:

Deu pra pegar a ideia?

Agora, confere esse exercício resolvido em vídeo do caso 2 👇👇👇

Caso 3: Fatores Quadráticos Distintos

Nesse caso os fatores do denominador são lineares e quadráticos irredutíveis, além disso os fatores quadráticos não se repetem. Como nesse exemplo aqui:

No denominador tem um termo linear: . O outro termo , é o que eu vou chamar de fator quadrático irredutível. Isso só significa que não tem como simplificar ele, não dá pra fatorá-lo em termos de fatores lineares, do tipo ou .

E uma maneira bem simples de testar se um termo quadrático é irredutível é calculando o discriminante (famoso ) e testando se ele é negativo. Nesse nosso exemplo, temos:

Pronto, deu negativo, então é um fator quadrático irredutível.

Ok, agora que vimos o que isso significa, vejamos como desmembrar nosso integrando lá em frações parciais:

Reparou a diferença?

Na fração correspondente ao termo quadrático, em vez de só um constante , apareceu um termo , beleza?

Caso 4: Fatores Quadráticos Repetidos

Esse caso meio que mistura tudo que vimos até aqui. Vamos ver integrais do tipo:

O termo quadrático no denominador é irredutível.

Montando as frações parciais:

E assim por diante!

Agora, vamos praticar com exercícios?!

Como Integrar por Frações Parciais?

Caso 1: Fatores Lineares Distintos

Caso 2: Fatores Lineares Repetidos

Caso 3: Fatores Quadráticos Distintos

Caso 4: Fatores Quadráticos Repetidos

Exercícios Resolvidos

Exercício Resolvido #1

James Stewart, Cálculo Vol. 1, tradução da 5ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2005, pp. 500 ex 26

Avalie a integral

∫ x 2 - x + 6 x 3 + 3 x d x

Passo 1

Temos novamente uma integral indefinida, de uma função racional, que não parece sair facilmente por nenhum método simples de integração que conhecemos. Nesse caso, aplicamos frações parciais.

Primeiro tenho que conferir se o grau do numerador é menor que o do denominador:

O polinômio do numerador tem grau 2 e o do denominador tem grau 3 →   check!

Agora eu vou fatorar o polinômio do denominador, isto é, achar suas raízes.

Então eu vou fazer isso aqui:

x 3 + 3 x = x x 2 + 3

Beleza, eu cheguei em um termo linear e em um termo que é quadrático. O que eu faço agora? Confiro se esse termo quadrático é um quadrático irredutível.

Δ = b 2 -   4 a c = 1 - 12 < 0

Como Δ < 0 , o termo é um quadrático irredutível e não há mais nada a fazer.

Beleza, e agora?

Passo 2

Vamos desmembrar em frações parciais, lembrando que o termo linear x não se repete então será desmembrado como A / x .

O termo quadrático irredutível também não se repete e, se repararmos bem, ele é um polinômio do tipo x 2 +   b x + c   com b = 0 . Sendo assim, podemos desmembrá-lo como A x + B x 2 + 3

x 2 - x + 6 x ( x 2 + 3 ) = A x + B x + C x 2 + 3

Fazendo o MMC:

x 2 - x + 6 x ( x 2 + 3 ) = A ( x 2 + 3 ) + ( B x + C ) x x ( x 2 + 3 )

x 2 - x + 6 = A x 2 + 3 A + B x 2 + C x

x 2 - x + 6 = x 2 A + B + x C + ( 3 A )

Resolvendo o sistema para achar as constantes:

A + B = 1         C = - 1       3 A = 6      

C = - 1   ;   A = 2 → B = - 1

Passo 3

Substituindo as constantes para integrar:

∫ x 2 - x + 6 x 3 + 3 x d x = ∫ 2 x d x - ∫ x + 1 x 2 + 3 d x = ∫ 2 x d x - ∫ x x 2 + 3 d x - ∫ 1 x 2 + 3 d x

Essas são, todas elas, integrais que podemos fazer diretamente. Não vou me estender na explicação de cada uma em si, qualquer dúvida basta olhar as teorias passadas. Basicamente, a segunda sai por substituição simples e a terceira você manipula para chegar na integral de uma trigonométrica inversa, beleza?

∫ 2 x d x - ∫ x x 2 + 3 d x - ∫ 1 x 2 + 3 d x = ∫ 2 x d x - 1 2 ∫ 2 x x 2 + 3 d x - 1 3 ∫ d x 3 x 3 2 + 1

2 ln ⁡ x - 1 2 ln ⁡ x 2 + 3 - arctan ⁡ x / 3 3 + C

Só não vai esquecer a constante de integral indefinida, hein?

- ''

Resposta

- 1 3 arctan ⁡ x 3   + 2 ln ⁡ x - 1 2 ln ⁡ x 2 + 3 + C

Exercício Resolvido #2

PUC-RJ - Cálculo B - P4 2014.2 - 1 h

h   ∫ x 2 5 x - x 2 d x

Passo 1

Polinômio sobre polinômio, isso geralmente é resolvido pela integral por frações parciais. Para isso, o grau do polinômio de cima tem que ser menor que o de baixo, então vamos dividir o cara de cima pelo denominador:

x 2 5 x - x 2 = x 2 - 5 x + 5 x 5 x - x 2

= - 1 + 5 x 5 x - x 2

Dá até para simplificar um x ali do segundo termo:

x 2 5 x - x 2 = - 1 + 5 5 - x

Então a integral fica assim:

∫ x 2 5 x - x 2 d x = ∫ - 1 + 5 5 - x d x

Passo 2

Agora pensando em resolver essa integral, o problema está só no segundo termo, já que a integral de - 1 já sabemos que será - x . Eu tinha dado a dica de fazer por frações parciais, mas esse cara que sobrou sai por substituição simples mesmo!

u = 5 - x → d u = - d x     ;   5 d x = - 5 d u

∫ 5 5 - x d x = ∫ - 5 d u u

= - 5 ln ⁡ u = - 5 ln ⁡ 5 - x

Então, a integral toda fica assim:

∫ x 2 5 x - x 2 d x = ∫ - 1 + 5 5 - x d x

= - x - 5 ln ⁡ 5 - x + C

Resposta

∫ x 2 5 x - x 2 d x = - x - 5 ln ⁡ 5 - x + C

Exercício Resolvido #3

James Stewart, Cálculo Vol. 1, tradução da 5ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2005, pp. 500 ex 38 – modificado

Avalie a integral

∫ x 4 + 1 x x 2 + 1 2 d x

Passo 1

Só para variar, uma integral indefinida, de uma função racional, que não parece muito amigável. Nesse caso, aplicamos frações parciais.

Primeiro tenho que conferir se o grau do numerador é menor que o do denominador:

O polinômio do numerador tem grau 4 e o do denominador tem grau 5 →   check!

O polinômio do denominador já parece estar na sua forma fatorada, certo?

Temos um x 2 ali, que é um termo linear x que aparece duas vezes, beleza?

Vamos conferir que aquele polinômio ali no denominador é irredutível?

Δ = b 2 -   4 a c = 0 2 - 4 ∙ 1 ∙ 1 = - 4 < 0

Como Δ < 0 , o termo é um quadrático irredutível e não há mais nada a fazer.

Show!

Passo 2

O termo quadrático irredutível se repete, percebe? Temos x 2 + 1 2 e, se repararmos bem, ele é um polinômio do tipo x 2 +   b x + c   com b = 0 . Sendo assim, podemos desmembrá-lo como

1 x 2 + 1 2 = B x + C x 2 + 1 + D x + E x 2 + 1 2

Então teremos:

x 4 + 1 x x 2 + 1 2 = A x + B x + C x 2 + 1 + D x + E x 2 + 1 2

Fazendo o MMC:

x 4 + 1 x x 2 + 1 2 = A x 2 + 1 2 + B x + C x x 2 + 1 + D x + E x x x 2 + 1 2

x 4 + 1 = A x 4 + 2 A x 2 + A + B x 4 + C x 3 + B x 2 + C x + D x 2 + E x

x 4 + 0 x 3 + 0 x 2 + 0 x + 1 = x 4 A + B + x 3 C + x 2 2 A + B + D + x C + E + ( A )

Resolvendo o sistema para achar as constantes:

A + B = 1       ( 1 )   C = 0       ( 2 ) 2 A + B + D = 0       ( 3 ) C + E = 0       ( 4 ) A = 1       ( 5 )

C = 0   ; A = 1   ; B = 0   ; D = - 2   ; E = 0  

Passo 3

Substituindo as constantes:

∫ x 4 + 1 x x 2 + 1 2 d x = ∫ 1 x + 0 x + 0 x 2 + 1 + - 2 x + 0 x 2 + 1 2 d x = ∫ d x x - ∫ 2 x d x x 2 + 1 2

Integrando essa bagaça (a segunda integral sai por substituição simples u = x 2 + 1 ), sem estresse!

∫ d x x - ∫ 2 x d x x 2 + 1 2 = ln ⁡ x + 1 x 2 + 1 +   C

E não esquece a constante porque é uma integral indefinida!

Resposta

∫ x 4 + 1 x x 2 + 1 2 d x = 1 x 2 + 1 + ln ⁡ x + C

Exercício Resolvido #4

UFRJ - Cálculo 1 - P2 2012.2 - 1d

Calcule as integrais abaixo:

∫ ln ⁡ x 3 + 1 x 3 d x

Passo 1

O enunciado nos pede para calcularmos uma integral indefinida. Ou seja, o resultado deve ser uma família de funções (Não esquecer da constante C )!

Olhando para a integral, vemos uma função logarítmica ( ln ⁡ x 3 + 1 ) e uma polinomial ( 1 x 3 ). Quando isso acontece, é interessante usar o método da integração por partes. Vamos lá!

Passo 2

∫ ln ⁡ x 3 + 1 x 3 d x

1. Chamar uma parte da integral de u e outra de d v . Devemos escolher u na seguinte ordem: função logarítmica ( ln ⁡ x ) > função inversa ( arcsen ⁡ x , arctg ⁡ x ,   … ) > função polinomial ( x n ) > função trigonométrica ( sen ⁡ x   x , cos ⁡ x , sec ⁡ x , ...) > função exponencial ( e x ).

u = ln ⁡ ( x 3 + 1 )     ( l o g a r í t m i c a ) d v = d x x 3 = x - 3 d x     ( p o l i n o m i a l )

2. Calcular d u derivando u . E calcular v integrando d v .

d u = 1 x 3 + 1 ⋅ 3 x 2 d x v = - 1 2 x - 2 = - 1 2 x 2

3. Fazer ∫ u d v = u v - ∫ v d u

∫ ln ⁡ x 3 + 1 x 3 d x = - 1 2 x 2 ln ⁡ x 3 + 1 - ∫ - 1 2 x 2 ⋅ 3 x 2 ⋅ 1 x 3 + 1 d x =

= - ln ⁡ x 3 + 1 2 x 2 + 3 2 ∫ 1 x 3 + 1 d x = - ln ⁡ x 3 + 1 2 x 2 + 3 2 I

4. Verificar se a integral ∫ v d u é possível de calcular. Se não, volte para o passo 1 e tente outro u e d v .

A integral I é uma divisão de polinômios, ou seja, pode ser calculada pelo método das frações parciais. Vamos aplicar o método para calculá-la.

Passo 3

I = ∫ 1 x 3 + 1 d x

1. Se o numerador tiver grau maior ou igual ao denominador, divida o numerador pelo denominador.

O grau do numerador ( 0 ) é menor do que o grau do denominador ( 3 ) .

2. Fatore o denominador para ele ficar na forma de um produto de termos.

1 x 3 + 1 = 1 ( x + 1 ) ( x 2 - x + 1 )

3. Desmembre a função racional em frações parciais com constantes nos numeradores.

1 ( x + 1 ) ( x 2 - x + 1 ) = A x + B x 2 - x + 1 + C x + 1

4. Faça o MMC, iguale os numeradores e agrupe as constantes.

1 ( x + 1 ) ( x 2 - x + 1 ) = A x + B x + 1 + C ( x 2 - x + 1 ) ( x + 1 ) ( x 2 - x + 1 )

1 = A x 2 + A x + B x + B + C x 2 - C x + C

0 ⋅ x 2 + 0 ⋅ x + 1 = A + C x 2 + A + B - C x + ( B + C )

Passo 4

5. Resolva o sistema para achar as constantes.

  A + C = 0           ( 1 )   A + B - C = 0           ( 2 )       B + C = 1           ( 3 )

De 1 : A = - C

Substituindo em 2 :   B - 2 C = 0 → B = 2 C

E voltando em 3 :   3 C = 1 → C = 1 / 3

Temos:

A = - 1 3 ; B = 2 3

6. Substitua as constantes e prepare para integrar.

∫ 1 x 3 + 1 d x = ∫ - 1 3 x + 2 3 x 2 - x + 1 d x + ∫ 1 3 x + 1 d x =

= - 1 3 ∫ x d x x 2 - x + 1 + 2 3 ∫ d x x 2 - x + 1 + 1 3 ∫ d x x + 1 =

= - 1 3 I 1 + 2 3 I 2 + 1 3 I 3

Passo 5

7. Calcular as integrais

Vamos calcular cada integral separadamente:

I 1 = ∫ x d x x 2 - x + 1

Completando o quadrado:

∫ x d x x - 1 2 2 + 3 4

Fazendo a seguinte substituição:

u = x - 1 2 → d u = d x   e   x = u + 1 2

Aplicando:

∫ u + 1 2 d u u 2 + 3 4 = ∫ u   d u u 2 + 3 4 + 1 2 ∫ d u u 2 + 3 4

Vamos fazer a seguinte substituição para a primeira integral:

t = u 2 + 3 4 → d t = 2 u   d u → u   d u = 1 2 d t

Aplicando:

1 2 ∫ d t t + 1 2 ⋅ ∫ d u 3 4 2 3 u 2 + 1 =

= 1 2 ln ⁡ | t | + 2 3 ⋅ 3 2 arctg ⁡ 2 3 u =

= 1 2 ln ⁡ u 2 + 3 4 + 3 3 arctg ⁡ 2 3 u =

I 1 = 1 2 ln ⁡ x 2 - x + 1 + 3 3 arctg ⁡ 2 x - 1 3

Calculando I 2 , vamos fazer de forma similar à integral anterior:

I 2 = ∫ d x x 2 - x + 1 = ∫ d x x - 1 2 2 + 3 4 =

= 4 3 ∫ d x x - 1 2 3 2 2 + 1 = 4 3 . 3 2 arctg ⁡ 2 x - 1 3

Calculando I 3 :

I 3 = ∫ d x x + 1 = ln ⁡ | x + 1 |

Passo 6

I = - 1 3 I 1 + 2 3 I 2 + 1 3 I 3 =

= - 1 6 ln ⁡ x 2 - x + 1 - 2 9 . 3 2 arctg ⁡ 2 x - 1 3 + 8 9 3 2 arctg ⁡ 2 x - 1 3 + 1 3 ln ⁡ x + 1 =

= - 1 6 ln ⁡ x 2 - x + 1 + 2 3 . 3 2 arctg ⁡ 2 x - 1 3 + 1 3 ln ⁡ | x + 1 |

Por fim:

∫ ln ⁡ x 3 + 1 x 3 d x = - ln ⁡ x 3 + 1 2 x 2 + 3 2 I =

= - ln ⁡ x 3 + 1 2 x 2 - 1 4 ln ⁡ x 2 - x + 1 + 3 2 arctg ⁡ 2 x - 1 3 + 1 2 ln ⁡ x + 1 + C

OBS: se você acertou esse exercício, parabéns! Grandes chances de você mandar bem na prova. Se não acertou, tente fazer de novo sem olhar. Esse problema é gigante, mas é só seguir os passos com calma e ir resolvendo as integrais conforme forem aparecendo. Acaba sendo muito útil chamar as diversas integrais de I 1 ,   I 2 ,     I 3 , etc e calculá-las separadamente. Isso vai te ajudar a se organizar. Vamo que vamo!

Resposta

∫ ln ⁡ x 3 + 1 x 3 d x = - ln ⁡ x 3 + 1 2 x 2 - 1 4 ln ⁡ x 2 - x + 1 + 3 2 arctg ⁡ 2 x - 1 3 + 1 2 ln ⁡ x + 1 + C

Exercício Resolvido #5

USP - Cálculo 1 - P3 2009 - 2 a

Calcule as seguintes integrais:

a   ∫ d x x + 1 x + 5

Passo 1

Ok, temos uma integral indefinida para resolver. De cara nós temos que dar uma mudada nessa cara do termo porque repara que aquele x + 5 ali tanto dando uma complicada na resolução. Vou tentar substituí-lo para ver se melhora a cara da integral:

u = x + 5 → d u = d x 2 x + 5

Acontece que na função nós não encontramos um termo perfeitamente igual ao d u que encontramos, para isso, fazemos a seguinte aprimorada:

d u = d x 2 x + 5 → d x = 2 d u x + 5

Como u =   x + 5 :

d x = 2 u d u

Agora, o x + 1 em função de u ficaria assim:

u = x + 5 → x + 5 = u 2

x + 1 = u 2 - 4

Agora vamos substituir:

∫ d x x + 1 x + 5 = ∫ 2 u d u u 2 - 4 u

= 2 ∫ d u u 2 - 4

= 2 ∫ d u u + 2 u - 2

Passo 2

Agora que já demos uma melhorada no vizu dessa integral, vemos que ela parece muito que vai sair por frações parciais, né não? E olha que beleza: o polinômio do denominador já está fatorado: ele está fatorado em um produto de dois termos lineares distintos. Esse aí é moleza de desmembrar em frações parciais:

1 u + 2 u - 2 = A u + 2 + B u - 2

1 u + 2 u - 2 = A u - 2 +   B ( u + 2 ) u + 2 u - 2

1 = A u - 2 +   B ( u + 2 )

Lembrando que, nesse caso, como só temos termos lineares, podemos utilizar aquele macetinho esperto de substituir x pelas raízes.

Para x = 2 :

1 = A   2 - 2 +   B ( 2 + 2 )

B = 1 4

Para x = - 2 :

1 = A - 2 - 2 +   B ( - 2 + 2 )

A = - 1 4

Passo 3

Agora substituímos as constantes para integrar:

2 ∫ d u u + 2 u - 2 = 2 ∫ - 1 4 d u u + 2 + 2 ∫ 1 4 d u u - 2

= 2 . ( 1 4 ) - ∫ d u u + 2 + ∫ d u u - 2

= 1 2 - l n   | u + 2 |   + l n   | u - 2 |   +   C 1

Utilizando as propriedades de logaritmo, temos:

= 1 2 l n   u - 2 u + 2   + C 1

Passo 4

Mas lembra que tínhamos feito uma substituição antes. A integral original é em x e não em u , então temos que voltar para x :

u = x + 5 . Então, finalmente, a resposta será:

= 1 2 l n   x + 5 - 2 x + 5 + 2   + C

Nem pensar em esquecer a constante, hein?

Resposta

∫ d x x + 1 x + 5 = 1 2 l n   x + 5 - 2 x + 5 + 2   + C

Exercício Resolvido #6

UFF - Cálculo IIA – GMA – 2008.2 – Lista 4 – 22

Calcule a integral indicada, fazendo uma substituição do tipo x = y n

∫ 2 x 1 + x 3 d x

Passo 1

Essa integral é deveras complexa hein, como será que podemos facilitar nossa vida? Olha a sugestão que ele deu, fazer aquela substituição serve para o que? Bem vai ajudar a tirar aquelas raízes da integral. A pergunta agora é: Qual valor de n devemos escolher!

Temos uma raiz cúbica e uma raiz quadrada, então esse n deve ser tal que tira as duas raízes, qual potência tem raiz cúbica e quadrada ao mesmo tempo? n = 6 , beleza?

Vamos fazer a substituição

x = y 6

E agora podemos aplicar o nosso passo a passo

Passo 2

Primeiro escolhemos a substituição

x = y 6

Calculamos sua diferencial

d x = 6 y 5 d y

Deixamos igual como está na integral. Neste caso já está igual.

Substituímos a integral

∫ 2 x 1 + x 3 d x = ∫ 2 y 6 1 + y 6 3 6 y 5 d y

∫ 2 y 3 1 + y 2 6 y 5 d y = ∫ 12 y 8 1 + y 2 d y

Caímos em uma equação que normalmente resolvemos por frações parciais, então vamos aplicar o seu passo a passo

Passo 3

Vamos ver os graus dos polinômios para ver se precisamos dividir essa fração antes de aplicar frações parciais

12 y 8 1 + y 2 ⇒ g r a u   8 g r a u   2

Como o grau de cima está maior que o grau de baixo, vamos precisar fazer a divisão.

Começamos dividindo o termo com x com maior expoente do numerador pelo termo com x com maior expoente do denominador:

12 y 8 y 2 = 12 y 6

Depois, multiplicamos a resposta pelo denominador:

12 y 6 ⋅ y 2 + 1 = 12 y 8 + 12 y 6

Depois, diminuímos o numerador pelo resultado obtido acima:

12 y 8 - 12 y 8 + 12 y 6 = - 12 y 6

Chegamos a uma nova divisão:

12 y 8 1 + y 2 = 12 y 6 - 12 y 6 y 2 + 1

Vamos colocar os termos que forem saindo de cada parte dessa divisão, de forma um pouco mais rápida, fizemos antes só para lembrar o método.

- 12 y 6 y 2 + 1 = - 12 y 4 + - 12 y 6 - - 12 y 4 y 2 + 1 y 2 + 1   = - 12 y 4 + 12 y 4 y 2 + 1

12 y 4 y 2 + 1 = 12 y 2 + 12 y 4 - 12 y 2 y 2 + 1 y 2 + 1 = 12 y 2 - 12 y 2 y 2 + 1

- 12 y 2 y 2 + 1 = - 12 + - 12 y 2 - - 12 y 2 + 1 y 2 + 1 = - 12 + 12 y 2 + 1

Vamos agora juntar tudo

12 y 8 1 + y 2 = 12 y 6 - 12 y 4 + 12 y 2 - 12 + 12 y 2 + 1

Passo 4

Vamos voltar para a integral, dessa vez não precisamos escrever as frações parciais porque o denominador já é um polinômio irredutível.

∫ 12 y 8 1 + y 2 d y = ∫ 12 y 6 - 12 y 4 + 12 y 2 - 12 + 12 y 2 + 1 d y

∫ 12 y 6 - 12 y 4 + 12 y 2 - 12 + 12 y 2 + 1 d y = 12 y 7 7 - 12 y 5 5 + 12 y 3 3 - 12 y + 12 arctan ⁡ y + C =

12 y 7 7 - 12 y 5 5 + 4 y 3 - 12 y + 12 arctan ⁡ y + C

Precisamos desubstituir o valor de y agora, lembra que

x = y 6

Então

y = x 1 / 6

Desubstituindo vai ficar

12 x 1 / 6 7 7 - 12 x 1 / 6 5 5 + 4 x 1 / 6 3 - 12 x 1 / 6 + 12 arctan ⁡ x 1 / 6 + C

12 x 7 / 6 7 - 12 x 5 / 6 5 + 4 x 1 / 2 - 12 x 1 / 6 + 12 arctan ⁡ x 1 / 6 + C

Resposta

12 x 7 / 6 7 - 12 x 5 / 6 5 + 4 x 1 / 2 - 12 x 1 / 6 + 12 arctan ⁡ x 1 / 6 + C

Exercício Resolvido #7

Calcule a integral

∫ cosh ⁡ x sinh ⁡ x + 4 cosh ⁡ x sinh ⁡ x 2 - sinh ⁡ x - 2 d x

Passo 1

Não sei você mas essa integral pra mim é de assustar. Mas relaxa, vamos com calma. Primeira coisa que temos que ver é que tem muitos termos repetidos. Por exemplo, podemos reescrever a integral dessa forma:

∫ cosh ⁡ x sinh ⁡ x + 4 cosh ⁡ x sinh ⁡ x 2 - sinh ⁡ x - 2 d x = ∫ cosh ⁡ x sinh ⁡ x + 4 sinh ⁡ x 2 - sinh ⁡ x - 2 d x

E assim, sobra dentro do colchetes somente termos com senh ⁡ x , o que é uma coisa boa se lembrarmos que:

d sinh ⁡ x d x = cosh ⁡ x

Então vamos tentar a substituição simples:

u = sinh ⁡ x

d u d x = cosh ⁡ x

d x = d u cosh ⁡ x

A nossa integral fica:

∫ cosh ⁡ x sinh ⁡ x + 4 sinh ⁡ x 2 - sinh ⁡ x - 2 d x = ∫ cosh ⁡ x u + 4 u 2 - u - 2 d u cosh ⁡ x

= ∫ u + 4 u 2 - u - 2 d u

Passo 2

Agora pra resolver a integral que sobrou, que é toda em função de u temos que usar as famosas e queridas frações parciais, beleza? Isso porque quando a gente consegue escrever na forma de frações parciais a integral já sai direto!

Vamos então achar as raízes do denominador pra gerar as frações. O denominador é:

u 2 - u - 2 = 0

Logo suas raízes vão ser:

u 1,2 = - - 1 ± - 1 2 - 4.1 . - 2 2

u 1,2 = 1 ± 1 + 8 2 = 1 ± 9 2 = 1 ± 3 2

u 1,2 = 2 - 1

Reescrevemos então o denominador para:

u 2 - u - 2 = u - u 1 u - u 2 = u - 2 u + 1

E a integral fica:

∫ u + 4 u 2 - u - 2 d u = ∫ u + 4 u - 2 u + 1 d u = ∫ A u - 2 + B u + 1 d u

= ∫ A u - 2 d u + ∫ B u + 1 d u = A ln ⁡ u - 2 + B ln ⁡ u + 1

Revertendo a substituição simples, ficamos com:

A ln ⁡ sinh ⁡ x - 2 + B ln ⁡ sinh ⁡ x + 1

Vai faltar só achar quem é A e B

Passo 3

Pra achar A e B , vamos lembrar do seguinte:

u + 4 u - 2 u + 1 = A u - 2 + B u + 1

Multiplicando a fração que contém A por u + 1 e a que contem B por u - 2 , ficamos com:

u + 4 u - 2 u + 1 = A u + 1 + B u - 2 u - 2 u + 1

Cortando os denominadores e aplicando a distributiva:

u + 4 = A u + A + B u - 2 B

Reorganizando:

1 u + 4 = A + B u + A - 2 B

E organizado dessa forma, se compararmos os coeficientes dos dois polinômios de primeiro grau acima, em função de u, que estão sendo igualados, obtemos esse sistema de equações esperto aqui:

A + B = 1 A - 2 B = 4

Multiplicando a primeira linha por 2:

2 A + 2 B = 2 A - 2 B = 4

Somando as duas linhas:

3 A = 6

A = 2

Mas como A + B = 1 , e A = 2 , teremos então que B = - 1 . Fechamos nossa questão! O resultado final vai ser:

∫ cosh ⁡ x sinh ⁡ x + 4 cosh ⁡ x sinh ⁡ x 2 - sinh ⁡ x - 2 d x =   A ln ⁡ sinh ⁡ x - 2 + B ln ⁡ sinh ⁡ x + 1 + C

∫ cosh ⁡ x sinh ⁡ x + 4 cosh ⁡ x sinh ⁡ x 2 - sinh ⁡ x - 2 d x =   2 ln ⁡ sinh ⁡ x - 2 - ln ⁡ sinh ⁡ x + 1 + C

Resposta

∫ cosh ⁡ x sinh ⁡ x + 4 cosh ⁡ x sinh ⁡ x 2 - sinh ⁡ x - 2 d x =   2 ln ⁡ sinh ⁡ x - 2 - ln ⁡ sinh ⁡ x + 1 + C

Exercícios de Livros Relacionados

Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ 8 x 2 + 8 x + 2 4 x 2 + 1 2d x
Expresse os integrandos como soma de frações parciais e calcule as integrais ∫ y 2 + 2 y + 1 y 2 + 1 2d y
Calcule.int (4)/(x^3 - x^2 - 2 x) d x
Faça uma substituição para expressar o integrando como uma função racional e então calcule a integral. ∫ s e n ( x ) cos 2 ⁡ x - 3 cos ⁡ x d x
Calcule a integralint (1)/((x - 2) (x^2 + 4)) d x