Continuidade de funções
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí meus jovens, nós somos o Responde aí, e estamos aqui com você hoje para falarmos sobre continuidade de funções.
Esse é um assunto que os professores de cálculo adoram demais e sempre aparece em provas.

O que é uma função contínua?
Existem duas maneiras de definirmos o que é uma função contínua: pelo gráfico ou pela definição hehe.
Vamos começar com o gráfico, que é mais simples kkk.
Visualmente é simples, sabe quando você pega pra desenhar alguma coisa, aí você vai passando o lápis na folha e não tira? Então, uma função contínua é aquela que você consegue desenhar o gráfico dela de forma contínua, sem tirar o lápis do papel. Um exemplo é essa função aqui:
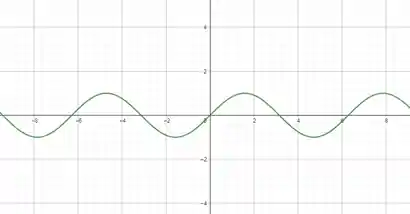
Ela é bem bonitinha, não é feita de pedacinhos separados, ela é exatamente como a palavra sugere, uma linha só, sem nenhuma descontinuidade.
Agora...
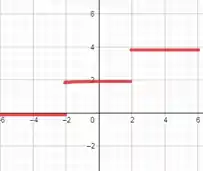
Imagine você riscando essa função, você começou do
Essas quebras mostram uma função descontinua.
E a definição matemática?
Essa parte é mais chatinha, mas é a parte que você vai usar na prova, então foca aqui!
Dizemos que uma função é contínua em um ponto
📢 ALERTA 1: Percebe que a definição de continuidade está muito atrelada ao conceito de limite, então caso você tenha alguma dúvida ou queira revisar esse assunto é só clicar aqui: Introdução aos limites e suas propriedades
Então, para analisarmos se uma função é contínua ou não precisamos avaliar duas coisas:
- O limite existe?
Dizemos que o limite de uma função tendendo a
📢 ALERTA 2: Os limites laterais são muito importantes também para a continuidade de funções, então se tiver alguma dúvida ou precisar até mesmo entender o que são limites laterais é só conferir essa nossa página aqui: Limites laterais e Existência do limite
Se essa condição for verdadeira, então o limite existe e seu valor é igual ao valor dos limites laterais.
- O limite é igual ao valor da função no ponto?
Uma vez que foi comprovado que o limite existe, devemos nos perguntar se ele é igual ao valor da função naquele ponto, pois se isso acontecer a função é contínua e se não acontecer a função não é continua.
Então, temos que verificar se:
Guarda essas duas perguntas no coração, combinado? São essas duas perguntas, nessa ordem, que você deve fazer para saber se uma função é ou não contínua.
Vídeo
É isso aí mesmo, nós temos o conteúdo também em vídeo. Confere aí:
Vídeo
Exercícios Resolvidos
Exercício Resolvido #1
CEFET - Cálculo 1 - P1 Roberto Sá 2012.2 – 3
Determine as constantes e para que a função abaixo seja contínua em .
Passo 1
Queremos fazer valer a continuidade nesse ponto, portanto:
Passo 2
Para que ela seja contínua nesse ponto, temos que garantir que seus limites laterais sejam iguais, bem como o próprio valor da função no ponto, ou seja:
Antes do , a função é dada pela lei . Bem no ponto ela vale , enquanto depois desse valor sua formação é dada por . Agora, basta resolver e matar o valor das constantes.
Passo 3
Bora testar os valores no limite?
Para B
Logo,
Resposta
Exercício Resolvido #2
UFF, Cálculo IA-Lista 5, GMA, 2008-1, Questão 21.
Verifique se a função é contínua no ponto indicado. Justifique a resposta.
Passo 1
Para que esse cara seja contínuo em precisamos que:
Já temos que . A questão se resume a verificar se
Também valerá .
Passo 2
Ao substituir cairemos numa indeterminação do tipo . Como encontramos ali duas diferenças, uma envolvendo raiz quadrada e outra envolvendo raiz cúbica, faz sentido calcular o limite através da multiplicação de seus conjugados. Para o termo de cima, teríamos:
Para o termo de baixo, com raiz cúbica, faremos o seguinte:
Passo 3
Voltando tudo ao limite:
Enfim, comprovamos que
E, portanto, a função será contínua.
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule o valor das constantes e para que a função abaixo seja contínua em .
Passo 1
Para que a função seja contínua em , precisamos que:
No caso, temos que:
Mas não somente isso, precisamos também garantir que o limite exista, e isso só ocorre se os limites laterais forem iguais, ou seja:
Passo 2
Portanto, fazendo pela esquerda:
Fazendo pela direita:
Portanto, para fugir da indeterminação nós calculamos ele pelo Limite Fundamental Trigonométrico:
Passo 3
Devemos ter então que:
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule a constante para que a função abaixo seja contínua:
Passo 1
No domínio , temos uma constante e um cosseno, sendo sua composição uma função contínua. Já no domínio , a função é uma composição de funções contínuas, já que polinômios e senos são contínuos, a raiz ali tem seu argumento positivo ou nulo, pois é a raiz de um número negativo vezes , e o único ponto onde o argumento do seno é descontínuo é , onde muda a lei de formação e observaremos com mais calma agora.
Resumindo: A função é contínua em . Para ela ser contínua, basta que achemos que ela é contínua também em .
Sabemos que, para que a função seja contínua em , precisamos que:
Passo 2
Aplicando pela direita o limite, temos:
Como se trata de uma função contínua:
Pelo lado esquerdo, temos:
Se tentarmos aplicar propriedades de limites, teremos um problema. Distribuindo o limite pelas funções:
O que acontece aqui é que não conseguimos avaliar o limite de , pois:
E não possuímos nenhuma informação acerca de . Essa função não é definida à medida que o vai para infinito ou menos infinito. O único jeito de atacar esse problema é com o Teorema do Confronto:
Independentemente do argumento do seno, essa relação acima vale. Multiplicando tudo por :
Puxando o limite:
Como temos que:
Pois a raiz é uma função contínua. Então segue que:
Gerando que
Passo 3
Substituindo no limite original, pelas propriedades de limites:
Portanto, como os limites tem que ser iguais:
Resposta
Exercício Resolvido #5
UFF - Cálculo IA - P1 Marlene 2013.2 – 3
Considere
Determine os pares ordenados de forma que essa função seja contínua em .
Passo 1
Para termos a função contínua em necessitamos que
Onde . Assim, queremos:
Passo 2
Começamos com o limite de valores menores que :
Tem uma cara de Limite Fundamental Trigonométrico, né? Vamos apostar nisso, forçar aparecer um embaixo e substituí-lo
Passo 3
Vamos calcular agora o limite para :
Nesse limite aí, repara que teríamos uma indeterminação dentro do seno e um fora:
Para resolver o problema do seno, uso o Teorema do Confronto com ele:
Agora basta calcular o seguinte:
Passo 4
Repara que esse cara pode ser multiplicado pelo seu conjugado para dar em alguma coisa função de seno:
Você deve lembrar que, pela relação fundamental da Trigonometria, . Com isso, colocando o seno ao quadrado em evidência teríamos:
Repara que eu multipliquei um em cima e embaixo, para poder aparecer o limite fundamental ao quadrado no primeiro cara:
Passo 5
Com isso, concluímos que
Logo,
E
Passo 6
Juntando o que calculamos, queremos:
Para os valores de , acharemos:
Como teríamos
Achamos os pares e , gerando que a função seja contínua em .