Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 20
Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Opa! O enunciado fornece uma função e um ponto e pede para justificarmos o motivo de não ser contínua nesse ponto:
Aqui nós vamos perceber que o comportamento da função se altera de forma abrupta quando nos aproximamos de , sendo que os limites laterais do lado esquerdo ) e pelo lado direito ).
Então para provarmos a descontinuidade em , devemos calcular tanto o limite como o valor da função em e compará-los.
Passo 2
Vamos calcular o limite de quando tende a . Quando tomamos o limite, nos aproximamos de por valores de próximos de porém nunca iguais a . Então, a expressão que devemos usar para o limite é . Substituindo 1 na equação, teremos:
Note que temos uma indeterminação do tipo 0/0. Para eliminá-la, vamos fatorar o numerador e o denominador.
Passo 3
Assim, o limite fica:
Como quando tomamos o limite, podemos simplificar o fator de modo que o limite fica:
Como , a função não é contínua em .
Passo 4
Para esboçarmos o gráfico da função, começaremos traçando a parte da função dada pela expressão
.
Aqui teremos um comportamento suave e contínuo, sem saltos ou descontinuidade. No caso de , marcamos um ponto no gráfico com coordenadas , pois a função assume o valor nesse ponto. Assim, teremos que o esboço do gráfico da função é:
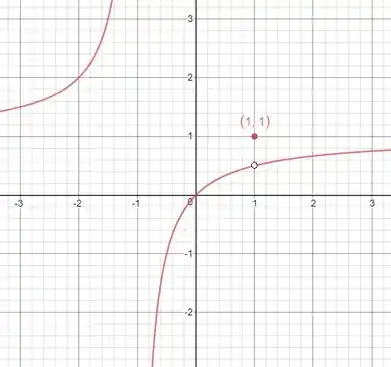
Prontinho!
Resposta
R: demonstração e esboço de gráfico.