Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 34
Localize as descontinuidades da função e ilustre com um gráfico.
Passo 1
O enunciado fornece a função e pede que localizemos as descontinuidades da função e esbocemos o seu gráfico.
Para isso, vamos utilizar os teoremas mostrados na seção do livro (teoremas 4, 5, 7 e 9).
O teorema 4 afirma que a soma, subtração, produto e quociente de funções contínuas é uma função contínua.
O teorema 5 afirma que todos os polinômios e funções racionais (quociente de polinômios) são funções contínuas em seus domínios.
O teorema 7 afirma que todas as funções raízes, trigonométricas, trigonométricas inversas, exponenciais e logarítmicas são contínuas em seus domínios.
Já o teorema 9 afirma que a composta de funções contínuas é contínua.
Vamos analisar os componentes da nossa função e assimilar os teoremas a cada um deles.
Veja só!
Passo 2
Pelo teorema 7, é uma função contínua em seu domínio.
Como produto de funções contínuas é uma função contínua (teorema 4), segue que é contínua em seu domínio.
Por fim, como é uma função contínua em seu domínio, segue que é uma função contínua em seu domínio.
Sacou?
Passo 3
Como é uma função contínua em seu domínio, suas descontinuidades serão os pontos que não pertencem ao domínio da função.
O domínio da função tangente são todos os números reais com excessão das raízes do cosseno:
Além disso, o domínio do logaritmo se restringe aos números positivos, de modo que é necessário que .
Todavia, é sempre um número não negativo, de modo que a relação só não será satisfeita se , ou ainda, se . Desta forma, devemos também excluir do domínio de as raízes tangente que são
Todas as raízes do cosseno e da tangente podem ser escritas simultaneamente como , com . Assim, o conjunto dos pontos de descontinuidade de é dado por
Tranquilo até aqui?
Passo 4
Para esboçar o gráfico de , vamos usar uma ferramenta gráfica.
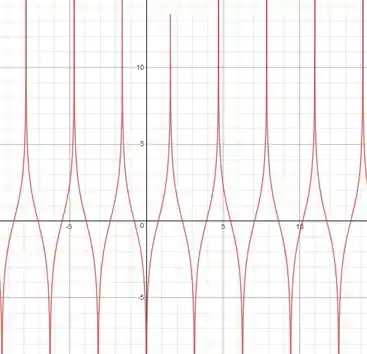
E aí! o que achou? Responde Aí!