Teorema do Valor intermediário
Produzido por Arthur Melo de AlmeidaTeoria
Bora bater um papo sobre o Teorema do Valor Intermediário?!
Aqui é no RespondeAí você vai aprender sobre Teorema do Valor Intermediário e todas aquelas matérias de exatas que te fazem perder o sono!
Então bora lá!
Também conhecido como Teorema de Bolzano ele diz que, para uma função
-Oiii?!
Pra ficar mais claro, eu vou te propor um desafio!
Eu quero que você tente com apenas uma linha, conectar os pontos da figura abaixo sem passar por
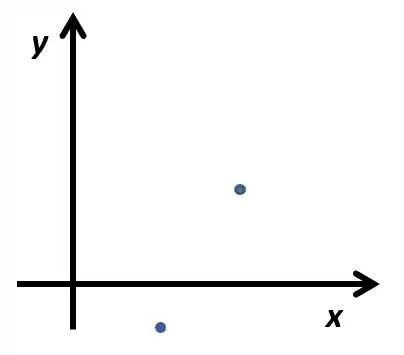
Essa reta (ou curva) vai ser nossa função
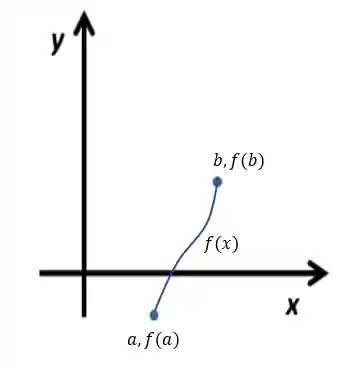
A função necessariamente vai cruzar o eixo
Teorema do Valor Intermediário: Raízes de uma função
Esse é um caso particular do Teorema do Valor Intermediário e para entende-la vamos usar a mesma imagem do exemplo anterior:
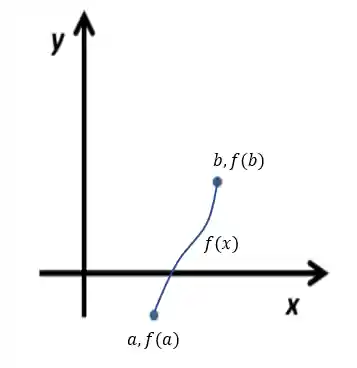
Uma consequência da definição do Teorema de Bolzano é que, se uma função contínua troca de sinal num certo intervalo, ela tem ao menos uma raiz real naquele intervalo.
Repare no desenho,
Exemplo:
Vamos então aplicar esse conceito na prática! Provando que
Como
-Simples assim? Só isso?
Sim!!
Teorema do Valor Intermediário: Raízes de uma equação
Imagine que eu te perguntasse se essa equação tem solução:
Mas você tem que provar pelo teorema do valor intermediário! Por onde você começaria?
Podemos manipular a equação e fazer:
Então podemos usar o TVI para verificar sobre a existência de raízes dela. Isso é a mesma coisa que procurar pontos onde as funções são iguais!
Ou seja, se você achar dois pontos em que
Ainda ficou com dúvida? Tem um vídeo aqui em baixo pra te ajudar!
Agora vamos fazer exercícios?!