Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.2 - Ex. 2

2 ) Calcule a área da região limitada pela curva x = t - sen t, y = 1 - cos t, 0≤ t ≤ 2π, e pelo eixo 0x

Passo 1

Primeiro temos que saber que região é essa que estamos integrando

x   =   t   -   s e n   t ,

  y   =   1   -   c o s   t ,  

0 ≤   t   ≤   2 π

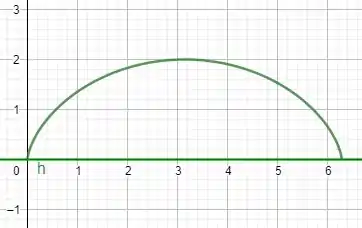
O problema é que as duas curvas, Tanto a elipse quanto O eixo x estão partindo de 0 e chegando a x = 2 π  

Contudo pelo que sabemos de circulação quando aprendemos o teorema de green, é que para calcularmos uma área a circulação deve ser anti-horaria. Podemos consertar isso então apenas botando um sinal negativo para a curva elíptica 😉

Passo 2

NO exercício 1, provamos que

k =   ∮ γ x   d y  

Agora vamos usar essa formula para calcular area que queremos. Então

k =   - ∮ γ 1 x   d y +   ∮ γ 2 x   d y

A curva γ 1 podemos definir como

x   =   t   -   s e n   t ,

  y   =   1   - cos ⁡ t

d y = s e n   t   d t  

A curva γ 2 podemos definir como

x = t

y = 0

d y = 0   d t

Vamos unir isso a nossa integração

k =   - ∮ γ 1   t   -   s e n   t s e n   t   d t   +   ∮ γ 2 t   .   0   d t

Ou seja

k =   ∮ γ 1 s e n 2 t   -   t s e n   t   d t  

Passo 3

O intervalo de integração está escrito no enunciado

0 ≤   t   ≤   2 π

Logo podemos escrever nossa área como

k =   ∮ 0 2 π s e n 2 t   -   t s e n   t   d t

k =   t 2 - s en ⁡ 2 t 4 - - t cos ⁡ t + sin ⁡ t 0 2 π

k = π +   2 π

k =   3 π

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∮ γ x   d y   = 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. Determinar a área entre as elipses:(a) x 2 + 9 y 2 - 2 x - 18 y + 1 = 0 e x 2 - 2 x + 4 y 2 - 8 y + 4 = 0 .
Nos exercícios 1 a 11, calcular as integrais curvilíneas dadas usand o teorema de Green.1. ∮ C l n x - 2 y d x + 2 x + e y d y , ao longo da elipse x 2 + y 2 9 = 1 , no sentido horário.
Nos exercícios 1 a 11, calcular as integrais curvilíneas dadas usando o teorema de Green.6. ∮ C f → ⋅ d r → , onde f → = - 3 x 2 y , 3 x y 2 e C é a circunferência x 2 + y 2 + 4 y = 0 , no sentido ant
14. Determinar a área entre as elipses:(a) 4 x 2 + y 2 = 4 e x 2 9 + y 2 4 = 1
Sejam B e γ como no Exercício 10. Prove queÁrea de B = - ∫ γ y d x