Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 8.2 - Ex. 6

6) Calcule

∮ γ - y x 2 + y 2 d x + x x 2 + y 2 d y

onde γ é uma curva fechada, C1 por partes, simples, fronteira de umconjunto B, cujo interior contém o círculo x 2   +   y 2   ≤   1 . (Sugestão. Apliqueo teorema de Green à região K compreendida entre a curva γ e acircunferência.)

Passo 1

Esse enunciado ficou um pouco confuso. Nossa região é essa

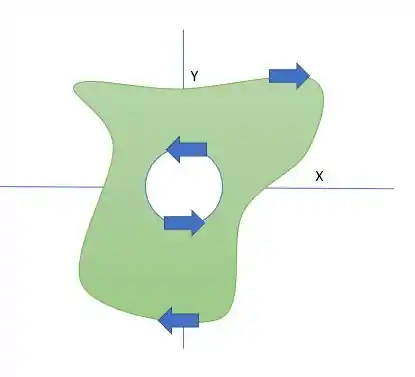
Alguma região disforme qualquer B que tem o interior x 2   +   y 2   ≤   1 vazio. E queremos a integral nessa área. A pergunta é, o que fazer ? Temos uma ótima dica do enunciado. Que é usar o Teorema de Green   ∮ γ 1 P d x + Q d y   +   ∮ γ 2 P d x + Q d y   = ∬ K ∂ Q ∂ x - ∂ P ∂ y   d x d y

Uma ideia para resolvermos essa integral é começar pelo lado direito desse teorema

∬ K ∂ Q ∂ x - ∂ P ∂ y   d x d y

Passo 2

Podemos fazer primeiro é calcular essas derivas parciais

P   =   - y x 2 + y 2

Q =   x x 2 + y 2      

Assim as derivadas parciais ficam

∂ Q ∂ x =   ∂ ∂ x x x 2 + y 2 → y 2 - x 2 x 2 + y 2 2

∂ P ∂ y =   ∂ ∂ y   - y x 2 + y 2 → y 2 - x 2 x 2 + y 2 2

Logo

∬ K y 2 - x 2 x 2 + y 2 2 - y 2 - x 2 x 2 + y 2 2   d x d y = 0

Passo 3

Okay. Isso pode ate parecer confuso, mas quer dizer que ate nos ajuda. Afinal tínhamos que

∮ γ 1 P d x + Q d y   +   ∮ γ 2 P d x + Q d y   = ∬ K ∂ Q ∂ x - ∂ P ∂ y   d x d y

Assim temos por fim

∮ γ 1 P d x + Q d y   +   ∮ γ 2 P d x + Q d y   = 0

∮ γ 1 P d x + Q d y   =   - ∮ γ 2 P d x + Q d y  

Podemos então calcular a região circular visto que é mais fácil ( e única forma de calcular essa integral )

∮ γ 2 P d x + Q d y  

Vamos parametrizar afinal nossa região é circular

x 2   +   y 2   ≤   1

x = cos ⁡ t

y = s e n   t

Assim nossas funções ficam

P   =   - y x 2 + y 2 →   -   s e n   t

Q =   x x 2 + y 2 → cos ⁡ t

d x =   - s e n   t   d t

d y = cos ⁡ t   d t  

Vamos unir isso a nossa integração

∮ γ 2 P d x + Q d y  

∮ 2 π 0 cos 2 ⁡ t + s e n 2 t   d t  

∮ 2 π     0   1 d t  

=   - 2 π

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∮ γ - y x 2 + y 2 d x + x x 2 + y 2 d y = 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.b. ∮ C 3 x 2 + y d x + 4 y 2 d y C é a fronteira do triangulo de vértices. 0,0 , 1,0 , 0,2
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.c. ∮ C e x - 3 y d x + e y - 6 x d y C é a elipse de equação x 2 + 4 y 2 = 1
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.e. ∮ C 2 x y - x 2 d x + x - y 2 d y C é a fronteira da região limitada por y = x 2 y 2 = x
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.d. ∮ C x - 1 e y d x + e y ln ⁡ x + 2 x d y C é a região limitada por x = y 4 + 1 x = 2
Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.f. ∮ C x + y d x + y - x d y C é a circunferência x 2 + y 2 - 2 a x = 0