Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 7
- Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando aumenta.
- Elimine o parâmetro para encontrar uma equação cartesiana da curva.
7.
Passo 1
- Queremos esboçar a curva que tem as equações paramétricas dadas. Bom, para fazer isso, vamos criar uma tabelinha de valores que relacionam , aí poderemos plotar esses pontos no gráfico.
- Agora nós precisamos eliminar o parâmetro , e escrever um equação cartesiana para a curva (isto é, com e ).
Assim, quando , por exemplo, teremos e . Fazemos o mesmo para outros valores de e montamos a seguinte tabela:
Show! Agora só precisamos colocar esses pontos em um gráfico e traçar uma linha unindo eles.
Passo 2
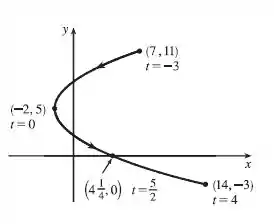
Passo 3
Para isso, vamos isolar em uma das equações e jogar esse valor dentro da outra equação. Desse jeito:
Mas agora não podemos esquecer de calcular qual o intervalo de e estamos calculando, pois está somente entre e .
Portanto, nossa equação cartesiana é , onde
Resposta
(b), onde
Exercícios de Livros Relacionados
Encontre a inclinação da reta tangente à curva polar dada em um ponto especificado pelo valor de θ . r = 2 + s e n 3 θ , θ = π / 4
Combine as equações polares com os gráficos com os gráficos I - V I . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.) r = l n θ,1 ≤ θ ≤ 6 π ; r = θ 2 ,0 ≤ θ ≤ 8 π ; r = c o s 3 θ ; r
Encontre a inclinação da reta tangente à curva polar dada em um ponto especificado pelo valor de θ . r = 2 c o s θ , θ = π / 3
Combine as equações polares com os gráficos com os gráficos I - V I . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.) r = l n θ,1 ≤ θ ≤ 6 π ; r = θ 2 ,0 ≤ θ ≤ 8 π ; r = c o s 3 θ ; r
Combine as equações polares com os gráficos com os gráficos I - V I . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.) r = l n θ,1 ≤ θ ≤ 6 π ; r = θ 2 ,0 ≤ θ ≤ 8 π ; r = c o s 3 θ ; r