Suponha que uma população cresça de acordo com o modelo logístico com capacidade de suporte e por ano.

(a) Escreva a equação diferencial logística para esses dados.

(b) Desenhe um campo de direções (à mão ou com um sistema de computação algébrica). O que ele lhe diz sobre as curvas solução?

(c) Use o campo de direções para esboçar as curvas solução para as populações iniciais de e . O que você pode dizer sobre a concavidade dessas curvas? Qual o significado dos pontos de inflexão?

(d) Programe uma calculadora ou um computador para usar o método de Euler com passo para estimar a população depois de anos se a população inicial for .

(e) Se a população inicial for , escreva uma fórmula para a população depois de anos. Use-a para calcular a população depois de anos e compare com sua estimativa na parte (d).

(f) Trace a solução da parte (e) e compare com a curva solução que você esboçou na parte (c).

(b) Agora vamos desenhar um campo de direções pra essa equação:

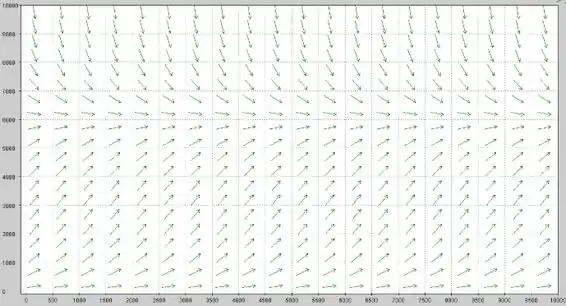
Olha que interessante, se você começar a seguir qualquer dessas setas, vai acabar parando no mesmo lugar, que é . Então isso nos diz que todas as soluções não nulas da equação diferencial se aproximam de uma solução de equilíbrio, quando

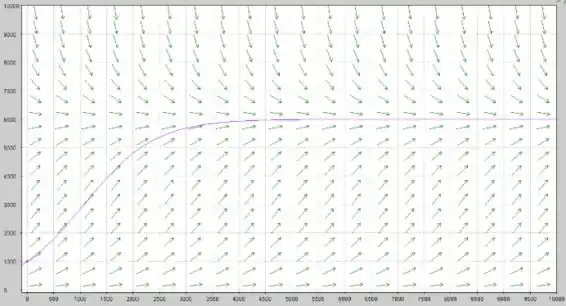
(c) Agora vamos esboçar algumas curvas solução, ok?

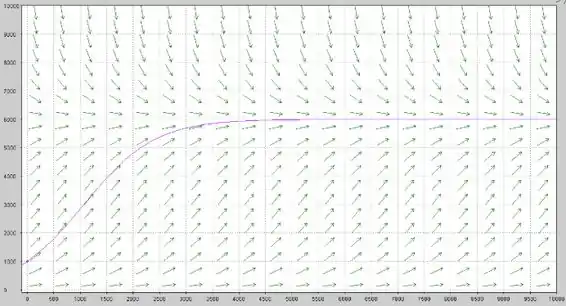
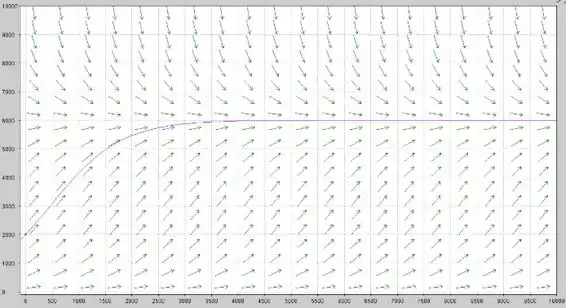
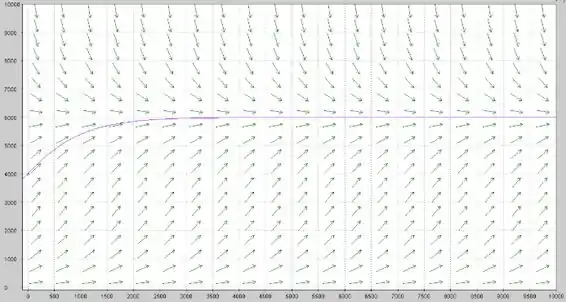
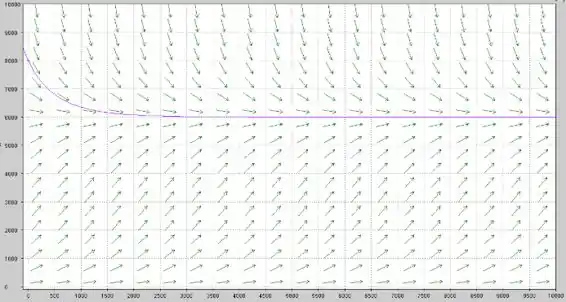
Repare uma coisa. Qualquer parte de qualquer curva que esteja abaixo de um certo por volta de tem concavidade voltada para cima. E acima desse mesmo , a concavidade fica pra baixo.

E esse tal ponto por volta de é justamente um ponto de inflexão. Isso significa que se a população estiver menor do que , a tendência é que a taxa de crescimento vá aumentando até chegar em E se passar desse ponto, a taxa de crescimento começa a diminuir. Não é que a população passa a diminuir, mas começa a crescer com menos velocidade, tá legal?

(d) Se programarmos um computador para usar o método de Euler com passo para estimar a população depois de anos, dado que a população inicial seja , obteremos o seguinte resultado:

(e) Galera, aqui a gente tem que escrever uma fórmula E como a gente consegue isso? Resolvendo a equação logística que a gente montou no item (a) !

Você pode escolher resolver essa equação específica ou recorrer à formula de para modelo logístico (que foi obtida resolvendo essa mesma equação logística, mas no caso geral) :

No nosso caso, temos e , então:

Agora vamos calcular a população depois de anos:

Arredondando para o inteiro mais próximo, tanto a resolução direta da equação diferencial quanto o método de Euler nos forneceram Beleza, pessoal?

(f) Agora vamos traçar o gráfico para a solução referente a :

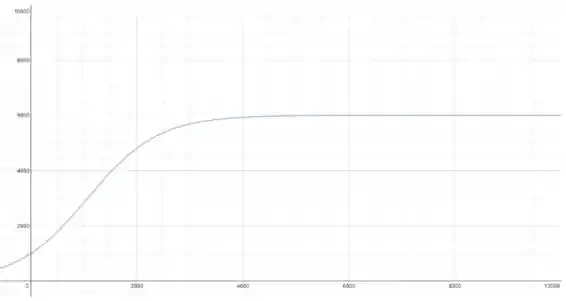
Compara com a curva que a gente já esboçou, não é muito semelhante?