Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 24
Resolva a equação e trace vários membros da família de soluções. Como a curva solução muda quando a constante varia?
Passo 1
Primeiramente, a gente verifica que a equação a ser resolvida é separável. Bora lá?
Agora a gente já pode integrar os dois lados:
Passo 2
Agora que já temos a nossa solução genérica, vamos traçar alguns gráficos dessa família de soluções, ou seja, vamos pegar alguns valores de e jogar na solução.
Mas para isso, atenção! Não podemos pegar qualquer valor de , pois a função
precisa estar definida!
De acordo com o que sabemos do domínio da função logaritmo, temos:
Logo, vamos escolher valores de maiores do que
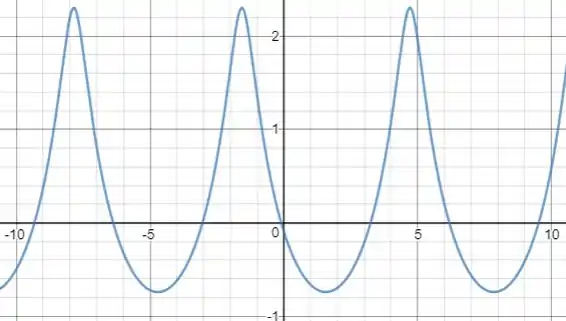
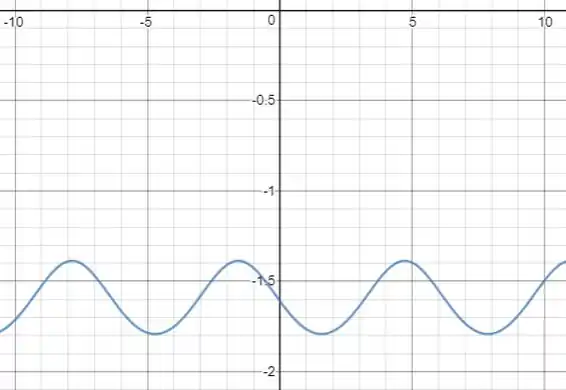
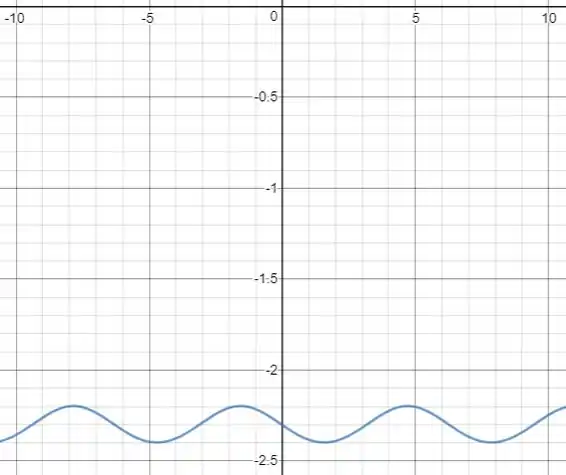
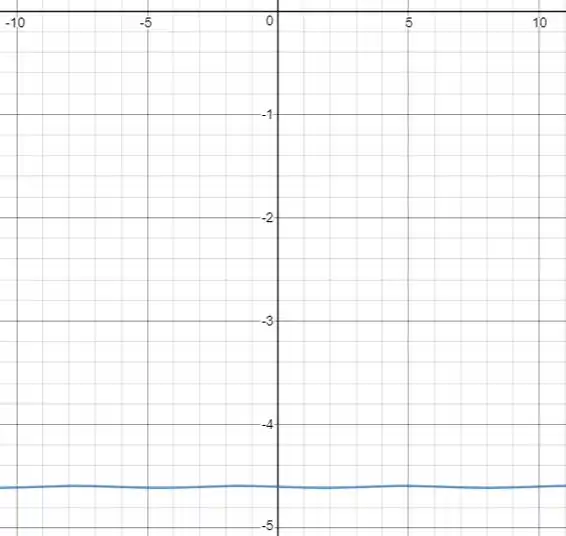
Passo 3
Agora, presta bastante atenção nos gráficos, o que você observa à medida que o valor de aumenta?
Parece que a amplitude dos gráficos, ou seja, a variação máxima entre as alturas de um mesmo gráfico, vai diminuindo.
Além disso, a curva solução também vai sendo deslocada para baixo.