Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 36
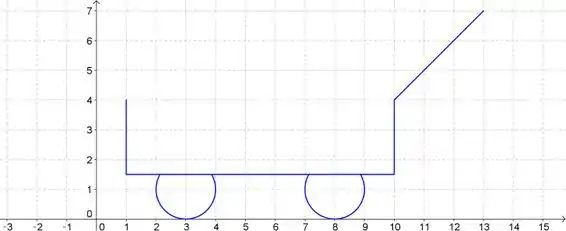
Use uma calculadora gráfica ou um computador para reproduzir a figura.
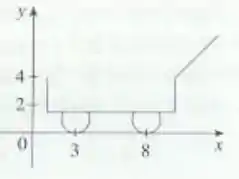
Passo 1
Olá, meu amigooo. Pronto para darmos início a mais uma resolução?
Aqui, eu e você deveremos utilizar um software gráfico para reproduzir a seguinte figura:
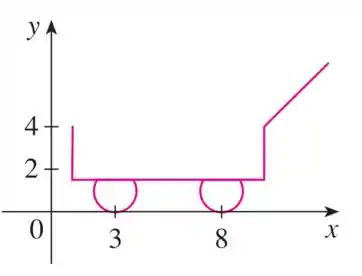
Para isso precisamos definir as equações paramétricas que representam cada um dos traços.
Veja que temos aqui, dois segmentos de reta na vertical, um segmento de reta na horizontal, um segmento de reta diagonal e 2 quase círculos.
Para conseguirmos encontrar equações para essa figura vamos precisar da equação de uma reta parametrizada em e :
E para as quase circunferências iremos utilizar a equação da circunferência:
Onde é o raio e é o centro da circunferência.
Passo 2
O segmento de linha vertical à esquerda vai de a .
O segmento de linha vertical à direita vai de a .
O segmento de linha horizontal vai de a .
O segmento de linha diagonal parece ter uma inclinação de e vai de a .
As rodas estão centradas em e e têm raio . Defina o intervalo de para a parte apropriada do círculo.
Colocando tudo isso no GeoGebra:
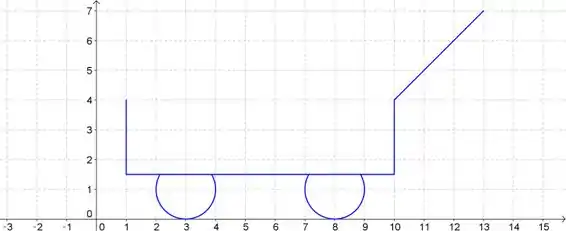
Resposta
