Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 8a
Se no exercício 7, temos uma hipociclóide de quatro cúspides ou astróide.
Passo 1
Antes de tudo, vamos utilizar a imagem para criar algumas possíveis visualizações que nos ajudarão daqui em diante:
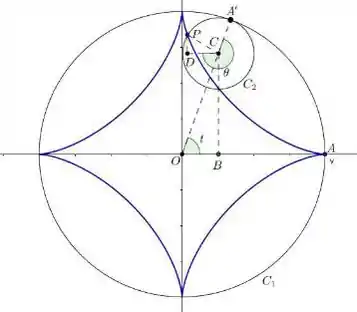
Passo 2
Além disso, analisando as informações que nós já temos é possível concluir que o raio da circunferência é igual a , sendo o raio da circunferência (uma vez que , onde é o raio de e é o raio de ). Sendo assim, tendo como ponto de partida de para a formação da curva temos que:
Passo 3
Tendo uma relação para é possível obter sobre as seguintes informações:
Passo 4
Com base naquilo que obtemos nos passos anteriores e com uma breve análise da imagem já somos capazes de identificar uma expressão que define :
E ao identificar a diferença entre os raios das duas circunferências:
Temos que:
Utilizando-se das relações trigonométricas sabe-se que:
Aplicando na equação obtemos o seguinte resultado:
Passo 5
Por outro lado, a expressão que define é:
Realizando a substituição dos termos por algumas das informações que já conhecemos, chegamos na seguinte expressão:
Da mesma maneira como no passo anterior, sabe-se a partir das relações trigonométricas que:
Para finalizar, substituindo na equação original obtemos o seguinte igualdade:
Resposta
Portanto, as equações:
Correspondem a parametrização de uma curva denominada astróide.