Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 2a
Faça um esboço das curvas definidas pelas seguintes funções vetoriais:
Passo 1
Esse item nos fornece a seguinte função vetorial:
Logo de cara nós já conseguimos ter uma ideia bem clara de que essa função se trata de uma reta paralela ao eixo , uma vez que os pontos de e se mantêm constantes enquanto o parâmetro varia.
Passo 2
Para termos certeza sobre a forma que imaginamos, vamos substituir o parâmetro por alguns valores do conjunto :
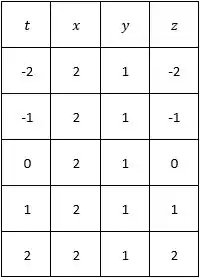
Resposta
Esboçando a curva a partir dos pontos presentes na tabela chegaremos em algo parecido com isso:
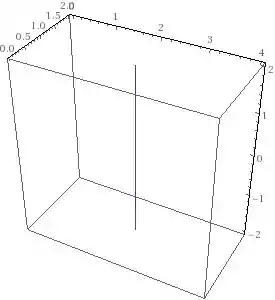
De fato, se trata de uma reta paralela ao eixo .
Exercícios de Livros Relacionados
Mostre que, se σ tt ∈ I é uma parametrização de uma reta, então σ ' ' t é paralelo a σ ' t .
Seja a função vetorial definida por: σ t = 2 t 1 + t 2 , 1 - t 2 1 + t 2 , 1 Mostre que o ângulo entre σ t e σ ' t é constante, isto é, independe de t .
Se a = 4 b no exercício 7 , temos uma hipociclóide de quatro cúspides ou astróide. (Veja um esboço da astróide na figura 1.13 . )b) Determine a equação cartesiana da astróide a partir de suas equações
Seja C a curva definida por σ t = 2 cos t,1 + 2 sen t . Determine uma equação da reta normal à curva no ponto 3 , 2
Escreva a equação da reta tangente à curva do I R 3 parametrizada por σ t = t , 1 - t 2 , 1 no ponto 0,1 , 1 .