Uma hipociclóide é a curva traçada por um ponto P sobre uma circunferência de raio b que gira dentro de uma circunferência fixa de raio a , a ≥ b . Suponha que a origem é o centro da circunferência fixa, A = ( a ,0 ) é um dos pontos em que P toca a circunferência fixa, B é o ponto móvel de tangência das duas circunferência e que o parâmetro θ é o ângulo A O B . Mostre que as equações paramétricas da hipociclóide são: x = a - b * cos ⁡ θ + b * cos ⁡ θ a - b b , y = a - b * sin ⁡ θ + b * sin ⁡ θ a - b b , θ ∈ [ 0 ,2 π ]

Portanto, o par de equações paramétricas da hipociclóide é: x = a - b * cos ⁡ θ + b * cos ⁡ θ b - a b , y = a - b * sin ⁡ θ + b * sin ⁡ θ b - a b , θ ∈ [ 0 ,2 π ]

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 7

Uma hipociclóide é a curva traçada por um ponto sobre uma circunferência de raio que gira dentro de uma circunferência fixa de raio , . Suponha que a origem é o centro da circunferência fixa, é um dos pontos em que toca a circunferência fixa, é o ponto móvel de tangência das duas circunferência e que o parâmetro é o ângulo . Mostre que as equações paramétricas da hipociclóide são:

Passo 1

Em primeiro lugar, vamos criar algumas visualizações:

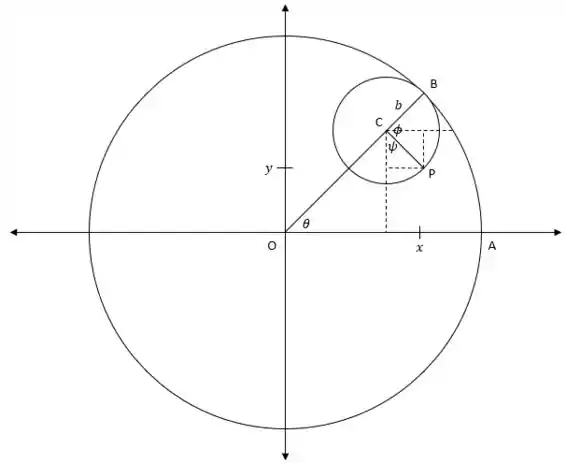
Passo 2

Tendo , com essas visualizações somos capazes de identificar como:

Para tornar as coisas mais fáceis devemos descobrir uma relação para o ângulo :

Aplicando a relação obtida em temos:

Porém, nós sabemos que:

Logo, temos que:

Passo 3

Mas isso ainda não está do jeito que nós queremos (em função apenas de ), então vamos pensar da seguinte forma:

Substituindo isso mais uma vez em :

Passo 4

A mesma lógica é utilizada para encontrarmos , que é obtida através da seguinte subtração:

Seguida das mesmas manipulações do passo anterior solucionadas para :

Resposta

Portanto, o par de equações paramétricas da hipociclóide é:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dê uma parametrização para cada uma das curvas.

Uma haste, presa na origem do plano x y , ocupa a posição da reta x = t y . A haste intercepta a reta y = 4 no ponto S e a elipse 4 x 2 + y - 2 2 = 4 no ponto Q . Quando t varia, o vértice P do triâng

Uma haste, presa na origem do plano x y , ocupa a posição da reta que faz um ângulo de θ radianos com o eixo positivo dos x . A haste intercepta a reta y = 2 a no ponto A e a circunferência x 2 + y -