Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 21
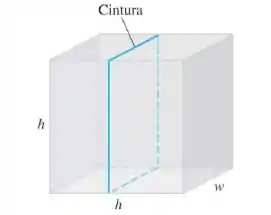
Suponha que, em vez de uma caixa com base quadrada, você possua uma caixa com lados quadraso cujas dimensões sejam e cuja cintura seja . Que dimensões darão À caixa o maior volume nessas condições?
Esboce o gráfico do volume em função de e compare o que se vê com a resposta dada no item
Passo 1
Olhando o desenho que ele deu,. Temos
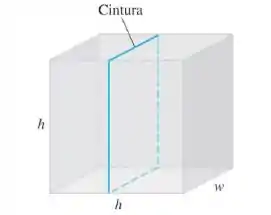
Vamos chamar o lado da base de e o comprimento de
O volume vai ser:
A soma que ele disse vai ser:
Logo:
O volume vai ficar:
O valor de pode ir de , até quando a cintura vale , fazendo ser , porque
Então:
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Fazendo isso igual a
Colocando o em evidência:
Vamos ter:
Ambos estão no intervalo.
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Vamos ter:
O maior dos valores é quando
Suas dimensões serão
E
Passo 4
Letra
Já fizemos em função de né? hahaha
Resposta
Lado do quadrado =
Comprimento =