Considere o seguinte problema: um fazendeiro com 300 m de cerca quer cercar uma área retangular e então dividi-la em quatro partes com cercas paralelas a um lado do retângulo. Qual é a maior área total possível das quatro partes?

1. Faça vários diagramas ilustrando a situação, alguns com divisões rasas e largas e alguns com divisões profundas e estreitas. Encontre as áreas totais dessas configurações. Parece que existe uma área máxima? Se a resposta for sim, estime-a.
2. Faça um diagrama ilustrando a situação geral. Introduza uma notação e marque no diagrama seus símbolos.
3. Escreva uma expressão para a área total.
4. Use a informação dada para escrever uma equação que relacione todas as variáveis.
5. Use a parte (d) para escrever a área total como uma função de uma variável
6. Acabe de resolver o problema e compare sua resposta com sua estimativa da parte (a)

Começando com a letra a, temos que fazer um diagrama, com divisões rasas e largas e com divisões profundas e estreitas. Depois disso precisamos encontrar as áreas de cada diagrama.

Temos de cerca, certo? E ela é dividida em partes retangulares e as cercas devem ser paralelas a um lado do retângulo. Percebe que tem infinitas formas de fazer isso?

Aqui a gente quer vários diagramas, entre eles temos que ter divisão rasa e larga e o profunda e estreita, não podemos esquecer que o nosso perímetro será :

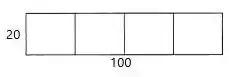
Então, estimando o perímetro:

E para a área, temos:

Pra facilitar a vida vamos sempre considerar os retângulos do mesmo tamanho, mas o enunciado não especificou nada, beleza?!

Com divisões profundas e estreitas, podemos ter essas configurações aqui, olha só:

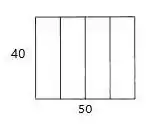
Dessa forma, teremos o perímetro:

E a área:

Vamos fazer mais uma:

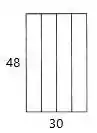
Com perímetro dado por:

E área dada por:

Beleza! O valor máximo que encontramos para a área entre essas configurações é:

Show! Agora podemos ir para a letra b!

Na letra b, precisamos fazer um diagrama pra adotar como geral e adotar variáveis. É claro que existem infinitas formas de fazer, mas vamos escolher essa aqui:

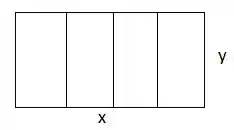
Sendo a base e a altura. Perceba que consideramos retângulos iguais, não vamos esquecer disso!

Agora na letra c, precisamos escrever uma expressão para a área:

Aqui na letra d, vamos escrever a equação que relaciona e . Assim, de acordo com a nossa informação do perímetro, temos que:

Na letra e, precisamos que essa equação da área tenha apenas uma variável, ok?

Pra fazer isso vamos usar a informação de perímetro dada e deixar em função de :

E substituindo isso na equação da área, temos:

Agora pra fechar vamos encontrar a área máxima, para isso vamos começar encontrando os valores críticos. Assim, derivando nossa expressão da área (), temos:

E igualando essa derivada a zero:

Obtemos:

O nosso valor máximo de área será substituindo esse valor de substituído na nossa equação:

Comparando com o valor de área que encontramos na letra (a), vemos que a área máxima é maior, certo?

Uhul!! Conseguimos!

Valeu, galera! Até a próxima! 😉