Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 2
Para a função representada graficamente aqui, determine os seguintes limites ou explique por que eles não existem
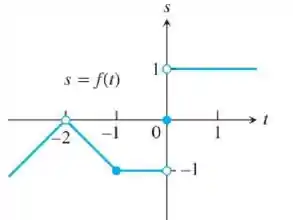
Passo 1
Questão envolvendo limite num ponto e gráfico só tem uma coisa a se fazer: olhar o gráfico da função um pouco a esquerda (vamos chamar isso de ) e um pouco a direita (vamos chamar isso de ) de .
Se os gráficos coincidirem, ótimo o limite existe e vale o valor do gráfico naquele ponto! Se não coincidir o limite não vai existir!
Passo 2
a) Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:
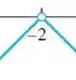
Olhando pela esquerda, vemos que a função se aproxima de 0, ou seja:
Olhando pela direita, vemos que a função se aproxima de 0, ou seja:
Como os limites deram iguais, temos que:
Passo 3
b) Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:
Olhando pela esquerda, vemos que a função se aproxima de -1, ou seja:
Olhando pela direita, vemos que a função se aproxima de -1, ou seja:
Tá vendo como deu igualzinho? Então o limite existe e vale:
Passo 4
c) Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:
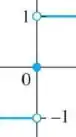
Olhando pela esquerda, vemos que a função se aproxima de -1, ou seja:
Olhando pela direita, vemos que a função se aproxima de 1, ou seja:
Tá vendo como deu diferente? Então o limite não existe!
Passo 5
d) Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:
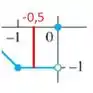
Olhando pela esquerda, vemos que a função se aproxima de -1, ou seja:
Olhando pela direita, vemos que a função se aproxima de -1, ou seja:
Como os limites deram iguais, temos que:
Resposta
a) 0
b) -1
c) Não existe
d) -1