Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.1 - Ex. 10

10. Distância percorrida rio acima Você está sentado junto à foz de um rio, observando as ondas levarem uma garrafa rio acima. Você registra a velocidade da garrafa a cada 5 minutos

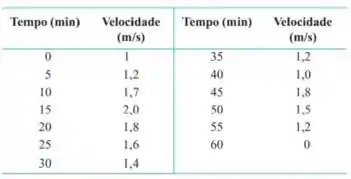
durante uma hora, obtendo os resultados apresentados na tabela a seguir. Que distância, aproximadamente, a garrafa percorreu durante essa hora? Faça uma estimativa usando 12

subintervalos de comprimento 5 com

a. valores na extremidade esquerda.

b. valores na extremidade direita.

Passo 1

Só precisamos aplicar na fórmula, apresentada no capitulo.

Vamos dizer que a velocidade se mantém constante, até que termine cada subintervalo. Após isso a velocidade vai aumentar para o próximo valor da tabela e continuar constante durante o subintervalo, até o próximo valor e assim sucessivemente até acabar os valores da tabela.

a.

Usando os valores da extremidade esquerda:

Obs: 5   m i n = 300   s

D = 1 300 + 1.2 300 + 1.7 300 + 2.0 300 + 1.8 300 + 1.6 300 + 1.4 300 + 1.2 300 + 1.0 300 + 1.8 300 + 1.5 300 + 1.2 300 = 5220   m

Passo 2

b.

Usando os valores da extremidade direita:

D = ( 1.2 ) ( 300 ) + ( 1.7 ) ( 300 ) + ( 2.0 ) ( 300 ) + ( 1.8 ) ( 300 ) + ( 1.6 ) ( 300 ) + ( 1.4 ) ( 300 ) + ( 1.2 ) ( 300 ) + ( 1.0 ) ( 300 ) + ( 1.8 ) ( 300 ) + ( 1.5 ) ( 300 ) + ( 1.2 ) ( 300 ) + ( 0 ) ( 300 ) = 4920   m

Resposta

a. 5220 m

b. 4920 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ 1 4 x - 2 d x (Teorema dado no livro)
Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ - 5 2 x + 5 x - 3d x (Teorema dado no livro)
Mostre que ∫ 0 1 xd x ≥ ∫ 0 1 x 2 d x , mas ∫ 1 2 xd x ≤ ∫ 1 2 x 2 d x .
Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ - π / 2 π / 2 3 sen 3 ⁡ xd x (Teorema dado no livro)
Aplique o Teorema 5.6.9 para encontrar um intervalo fechado contendo a integral definida dada: ∫ - 1 4 ( x 4 - 8 x 2 + 16 )d x (Teorema dado no livro)