Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.6 - Ex. 41
Mostre que , mas .
Passo 1
Já vimos que se temos em um intervalo duas funções e integráveis e se no intervalo, isso implicará que . Basta então comparar as funções e nos intervalos dados para tentar provar o que se pede.
Passo 2
Os gráficos da reta e da parábola são facilmente esboçados no intervalo , como mostra a imagem:
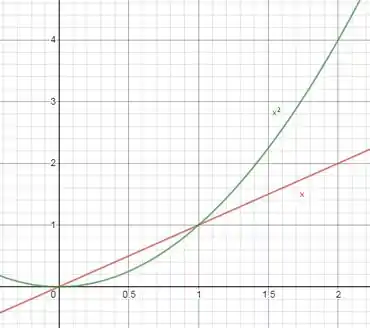
Como vemos, temos para o intervalo a desigualdade e para a desigualdade . Com isso, fica provado que e .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja f : 0,1 → R dada por f ( x ) = xs ex∈Q0s ex∉Q Verifique que se os c i forem racionais ∑ i = 1 n f c i △ x i tende a 1 2 , quando m a x△ x→ 0 .Prove que f não é integrável em 0,1 .
38. Prove que a função maior inteiro é descontínua em [ 0 , 3 2 ] e mesmo assim é integrável nesse intervalo. Mostre também que ∫ 0 3 / 2 x d x = 1 2
37. Prove que a função sinal é descontínua em [ - 1,1 ] e mesmo assim é integrável nesse intervalo. Mostre também que ∫ - 1 1 s g n xd x = 0
Expresse como uma integral definida: lim n → + ∞ ∑ i = 1 n n i + n 2 Sugestão: considere a fução f para a qual f x = 1 x 2 em [ 1,2 ] .
Expresse como uma integral definida: lim n → + ∞ ∑ i = 1 n 8 i 2 n 3 Sugestão: considere a fução f para a qual f x = x 2 .