Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.4 - Ex. 10
10. Encontrar o trabalho de uma força variável dirigida à origem das coordenadas, cuja grandeza é proporcional ao afastamento do ponto em relação a origem das coordenadas, se o ponto de aplicação dessa força, descreve no sentido anti-horário, a parte da elipse no quadrante.
Passo 1
Bom! Vamos pra mais um probleminha de integral de linha! Nós queremos trabalhar com a seguinte integral:
E a nossa força , como sabemos que é proporcional ao afastamento do ponto em relação a origem das coordenadas; é dada por:
Onde é uma constante de proporcionalidade. E você deve estar se perguntando. Por que a força tem componentes negativos?
É simples! A força está dirigida à origem das coordenadas. Por isso, devemos inverter os sinais, já que aponta no sentido oposto ao que seria o sentido positivo de nosso referencial.
Encerrada essa pequena introduçãozinha; vamos pro que realmente interessa. Bora tratar de parametrizar a curva , que é dada por:
E então, vamos tentar trabalhar um pouco mais em cima dessa expressão. Bora dividir tudo por :
Isso aí é uma elipse de centro na origem e mais achatadinha em , por .
Agora, como sabemos que nossa curva é uma elipse, vamos nos lembrar do jeito pelo qual as elipses, com o formato são parametrizadas:
Como e no nosso caso, então...
Logo. Uma boa parametrização é:
Passo 2
O próximo passo agora, é justamente mudar a função que nos é fornecida para os termos dessa parametrização que obtivemos.
Olha só! A nossa função é dada por:
E para fazer a troca na função para os termos parametrizados, basta realizar a substituição no , com os valores que temos lá do :
Pronto! Já temos uma função inteira em termos de .
Passo 3
O passo número três consiste em encontrar o termo fazendo:
Ou seja, o que temos que fazer é apenas tirar a primeira derivada de . Vamos lá:
Passo 4
Pronto! Só nos resta pegar os três ingredientes que já encontramos e substituir na integral:
Pera! Mas quais são esses limites de integração?
Presta atenção! O enunciado nos diz que a trajetória é descrita no sentido anti-horário, no quadrante.
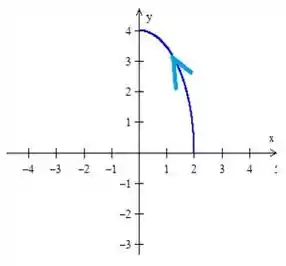
Ou seja, o nosso limite de integração vai de até :