Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.2 - Ex. 51
Um objeto se move sobre a curva , mostrada na figura abaixo, de a . Os comprimentos dos vetores do campo de força são medidos em newtons pela escala nos eixos. Estime o trabalho realizado por sobre o objeto.
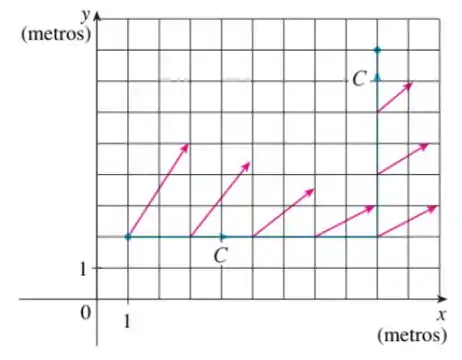
Passo 1
E aê, galera, tudo bem?
A questão nos deu uma imagem a respeito de uma curva que vai de a e quer o trabalho realizado pelos comprimentos dos vetores do campo de força . Belê?
Pra mostrar calcular o trabalho, primeiro vamos relembrar sua fórmula tradicional:
Mas também podemos escrever em termos do vetor tangente :
Assim temos que o trabalho realizado vai ser a soma de todas as contribuições de ao longo da curva .
Passo 2
Todas as contribuições da força em cada pedaço estão marcadas aqui embaixo ó:
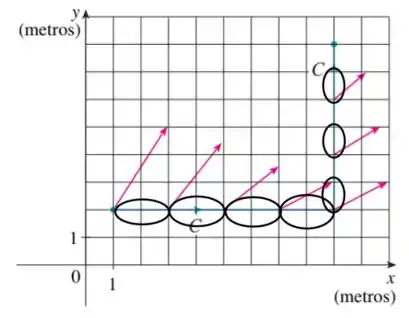
Temos três contribuições valendo e quatro contribuições valendo .
E o ? Bom, ele é constante e vale pela escala, saca só (em verde):
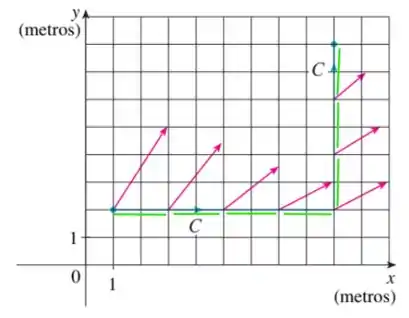
Então temos pedacinhos valendo cada.
Passo 3
Legal! O próximo passo é somar todas as contribuições:
Então o trabalho realizado é aproximadamente , show? 😉