Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 11
11. Determine o volume do sólido gerado pela rotação da região "triangular" limitada pelo eixo x, pela reta e pela curva no primeiro quadrante em torno do eixo x.
Passo 1
Vamos desenhar a função tangente de 0 até , para podermos enxergar o que estamos calculando:
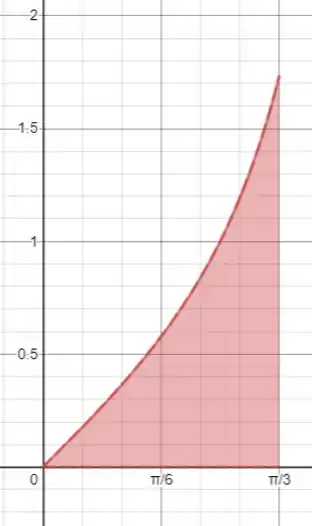
Precisamos calcular, então, o volume do sólido gerado pela revolução desse “triângulo”.
Passo 2
Para calcular o volume vamos usar o método do disco, em que a função vai ser igual ao raio
A área desse disco será igual a
Agora é só aplicar na fórmula
Iremos integrar a função de até :
Vamos usar a identidade trigonométrica
e reescrever a equação:
Integral de 1 é e a integral de é , então o volume fica:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido resultante se a região sob a curva y = 1 x 2 + 3 x + 2 de x = 0 até x = 1 for girada em torno do:b) eixo y ;
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = e x ,y = 0 ,x = 0 ,x
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 / x ,x = 1 ,x = 2
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x ,y = 0 ,x = 2 ,x =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = ln x ,y = 1 ,y = 2