Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 16
16. Volume de uma bola de futebol americano O perfil de uma bola de futebol americano se assemelha à elipse mostrada aqui. Determine o volume aproximado da bola de futebol até a
polegada cúbica mais próxima.
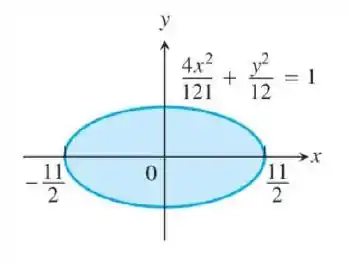
Passo 1
Usando o método do disco conseguimos encontrar, facilmente, o volume.
Vamos precisar da função , pois ela será o raio do nosso disco, isolando
Então nosso raio é
A área do disco é
Os limites de integração estão no próprio gráfico, e
Aplicando na fórmula:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x 2 / 3 ,x = 1 ,y =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y 2 = x ,x = 2 y ;e mt
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 x ,y = 0 , x = 1 ,
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = x ,y = x ;e mt o r
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 1e mt o r n od eO C