Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.1 - Ex. 12
12. Distância a partir dos dados de velocidade A tabela a seguir fornece dados sobre a velocidade de um carro esportivo que acelera de 0 a 142 milhas/hora em 36 segundos ( 10 milésimos de uma hora).
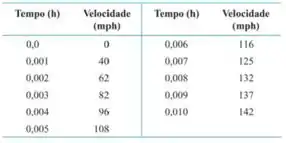
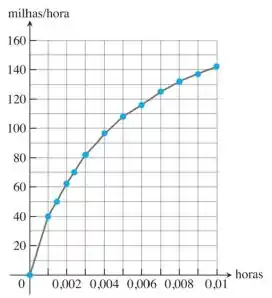
a. Use retângulos para estimar a distância que o carro percorreu durante os 36 segundos decorridos até atingir 142 milhas/hora.
b. Aproximadamente quantos segundos o carro levou para atingir o ponto médio do caminho? Qual era então a velocidade aproximada do carro?
Passo 1
a.
Podemos usar 10 retângulos para fazer um cálculo aproximado da distância percorrida.
Vamos usar valores aproximados para as alturas do ponto médio das velocidades.
Passo 2
b.
Antes de tudo, vamos descobrir quanto é a metade do caminho:
Agora vamos ver quanto que o carro percorreu a cada retângulo:
1º:
2º:
3º
4º
5º
6º
Perceba que agora ele não ira percorrer mais um retângulo inteiro, então vamos calcular quanto desse retângulo ele vai percorrer, para chegar nessa distância:
Falta uma distância de:
Logo, o tempo que ele ainda precisa é de:
O tempo total necessário vai ser de:
Resposta
a.
b.