Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.8 - Ex. 12

12)

Sobre uma partícula que se desloca sobre o eixo Ox atua uma força F → , sempre dirigida para o ponto P (veja a figura), e cuja intensidade é igual ao inverso do quadrado da distância da partícula a P .

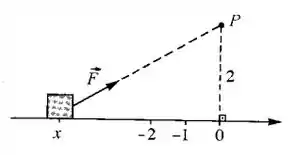
Calcule o trabalho realizado por F → quando a partícula se desloca de x = - 2   a x = - 1 .

Passo 1

Lá da física, a gente sabe o seguinte:

τ = ∫ a b f x c o s θ   d x       ( * )

Então precisamos resolver essa integral pra achar o trabalho!!

Passo 2

Primeiro vamos trabalhar nesse triangulo (ABC)!

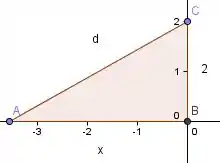
Aplicando o teorema de Pitágoras em ABC:

d 2 =   2 2 + x 2   =   4 + x 2 i

Pelo enunciado,

f d = 1 d 2

Usando a relação i :

f d = 1 d 2   →   f x = 1 4   + x 2   ( i i )

Além disso,

c o s θ = - x d = - x 4 + x 2   ( i i i )

Passo 3

Juntando as relações ( i i ) e ( i i i ) :

τ = ∫ a b f x c o s θ   d x   = ∫ - 2 - 1 1 4 + x 2 ⋅ - x 4 + x 2 d x =   ∫ - 2 - 1 - x 4 + x 2 ⋅ 4 + x 2 d x  

Agora vamos resolver essa integral!

Primeira vamos fazer uma substituição de variável

u = 4 + x 2

Derivando,

d u = 2 x   d x que é basicamente d u 2 = x d x

Não esquece: Se fizemos uma substituição, então temos que mudar os limites de integração!!!

x = - 2   → u = 8

x =   - 1 → u = 5

∫ - 2 - 1 - x 4 + x 2 ⋅ 4 + x 2 d x   = - ∫ 8 5 1 u u d u 2 = - 1 2 ⋅ ∫ 8 5 d u u 1 + 1 2  

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c     quando   n   ≠ - 1  

- 1 2 ⋅ ∫ 8 5 d u u 3 2 = - 1 2 ⋅ u - 3 2 + 1 - 3 2 + 1 | 8 5 = - 1 2 ⋅ ( u - 1 2   | 8 5 ) - 1 2   = - 1 2 ⋅ - 2 ⋅ 1 5 -   1 8

Fechamos, vamos ter:

τ = 1 5 -   1 8

Resposta

τ = 1 5 -   1 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

22.Um Reservatório é da forma de um paralelepípedo retângulo de 1,40m de profundidade, 4m de largura e 8m de comprimento. Encontrar o trabalho necessário para bombear a água do reservatório ao nível d
19.Um tanque cilíndrico reto de raio de 1,2 m e altura 3 m está cheio de água. Achar o trabalho efetuado para esvaziar o tanque, pela parte superior.
21.Um tanque tem forma de um cone circular reto, de altura20m e raio da base 102 cm. Se o tanque está cheio de água, encontrar o trabalho realizado para bombear a água pelo topo do tanque.
20. Um tanque cilíndrico circular reto de 2m de diâmetro e 3m de profundidade está cheio de água e deve ser esvaziado pela parte superior. Determinar o trabalho necessário para esvaziar o tanque:a) Co
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O trabalho e a energia cinética têm as mesmas unidades no sistema MKS.