Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 13
13. Determine o volume do sólido gerado pela rotação da região limitada pela curva e pelas retas , e em torno do eixo .
Passo 1
Se nós desenharmos a função vamos observar que não conseguimos pegar um disco a partir de :
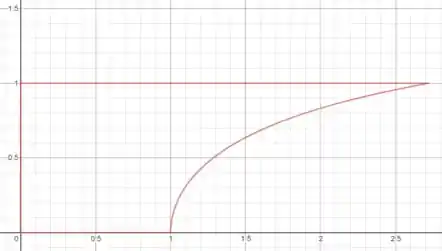
O que podemos fazer é calcular o volume gerado pela revolução dessa área:
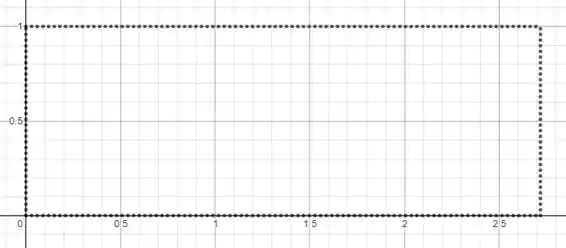
E tirar o volume gerado pela revolução dessa área:
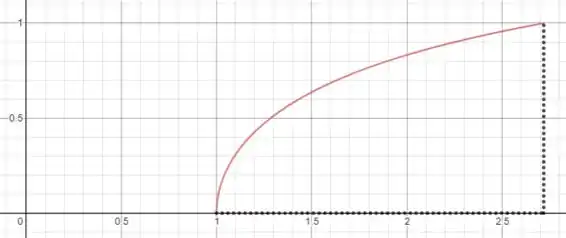
Desse jeito as contas vão ficar mais fáceis.
Passo 2
Quando a gente faz a revolução de um retângulo vamos obter um cilindro.
-Nesse caso seu raio vai ser igual a 1, pois é esse seu tamanho em
-Sua altura vai ser seu tamanho em , que precisamos descobrir, podemos fazer isso encontrando a coordenada da curva quando :
Portanto o volume desse cilindro é igual a
Passo 3
Já o volume do solido gerado a partir da revolução dessa área:
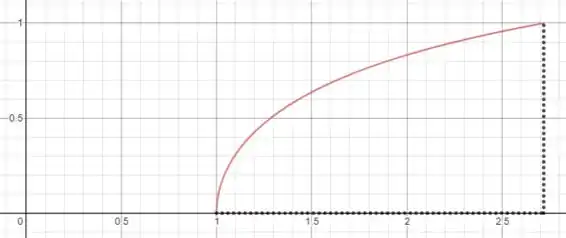
é um pouco mais chatinho de resolver.
Seu raio vai ser o valor da curva, então para sabermos qual é esse valor precisamos isolar a variável na equação:
Aplicando o logaritimo:
Então o raio do disco é igual a
Agora precisamos calcular a área do disco:
Aplicando na fórmula do volume:
(Cuidado com os limites de integração, aqui a gente tem que ir de 1 até )
Perceba que a se derivarmos essa função:
vamos obter . Portanto a integral do é igual a
Gente eu sei que esse passo ai foi meio mágico, mas pra resolver essa integral, a gente precisa de uma técnica que vai ser aprendida no capitulo 8, integração por partes. Continuando as contas
Passo 4
Para terminar vamos subtrair esse ultimo volume calculado do volume do cilindro e assim obter o volume do sólido que estamos querendo: