Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 16
13-16. Esboce a região cuja área com sinal é representada pela integral definida e calcule a integral usando uma fórmula apropriada de Geometria quando for necessário.
16.
(a)
(b)
(c)
(d)
Passo 1
Vamos lá! A ideia é desenharmos esses gráficos e utilizarmos a nossas fórmulas de geometria plana para conseguirmos calcular a área, caso não lembre da fórmula, sem problemas, vou te lembrando no caminho.
Sem mais enrolação...
Na letra a), temos uma função constante , então é uma reta paralelo ao eixo . Calmaaa, eu vou desenhar o gráfico!
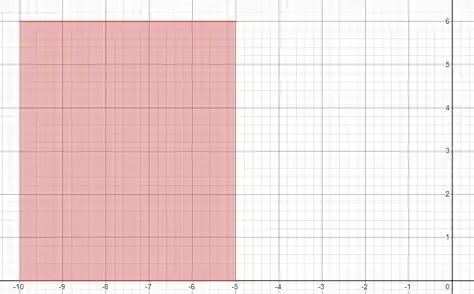
Essa figura é um retângulo e a área de um retângulo é dado por
Ora, a base é o comprimento daquela reta que vai de até , então
Já a altura é a comprimento do segmento que vai de até , então a
Calculando a área, temos:
Sabemos que a integral é numericamente igual a área, então temos:
Vamos para a letra b),
Vamos desenhar o gráfico da função seno.
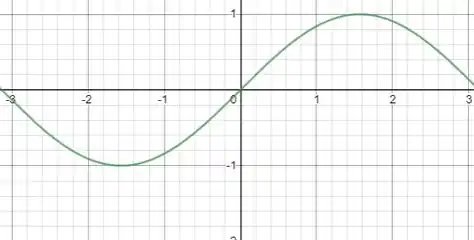
Beleza!! Só que temos que pegar os valores de entre e . Então fica assim:
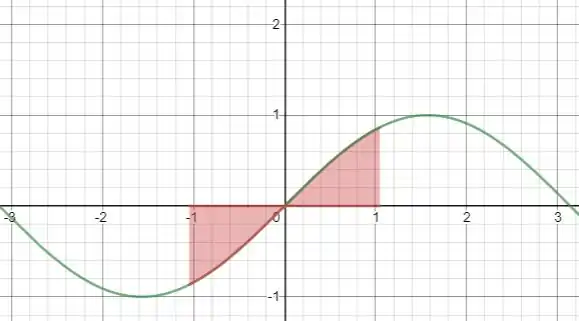
Só que se você sabe que a função seno é simétrica à origem, pois é uma função ímpar, mas no que isso nos ajuda?
Ora, tudo que está a direita delimitado por e é igual ao que está a esquerda que é delimitado por e .
Portanto a área da região em vinho à esquerda é igual a área á direita, então a área líquida é igual a !!
Só que nesse nosso exercício a área é numericamente igual a integral, portanto
Passo 2
Vamos para a letra c)!
É uma função modula e como toda função modular temos que rebater o gráfico da função que está dentro, mais ou menos assim:
Agora rebatendo, temos:
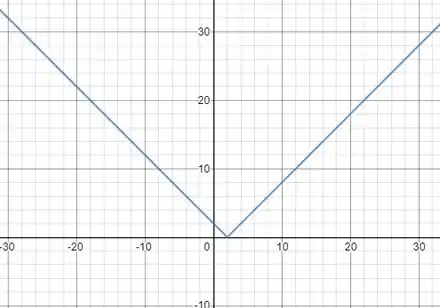
Queremos a região acima do eixo e entre os pontos e .
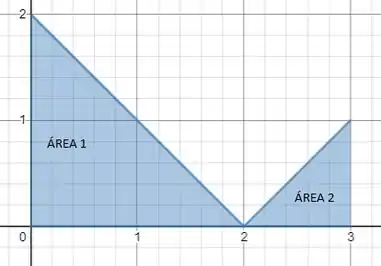
A área de um triângulo é dada por:
Vamos começar com área 1, temos que a altura vai de até , então e a base a mesma coisa, vai de até , então .
Calculando a área, temos:
Vamos para a área 2, temos que a altura vai de até , então e a base a mesma coisa, vai de até , então
Calculando a área, temos:
Então para calcularmos a área total, temos que somar essas duas áreas:
Sabemos que a integral é numericamente igual a área, então:
Passo 3
Agora para finalizar! Ufaaaaaa! Vamos para a letra d)
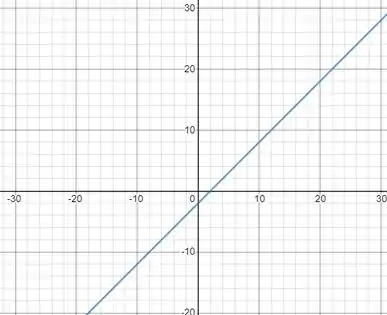
Então temos que desenhar o gráfico de , daqui tiramos que e, desenhando esse gráfico, temos:
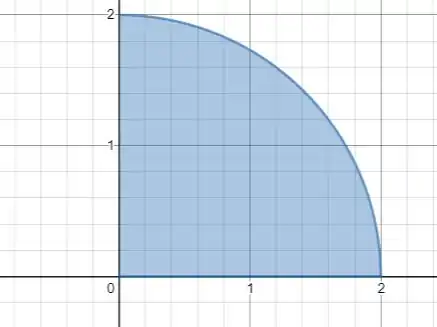
Que é a quarta parte de uma circunferência de raio , a área de uma circunferência é , então a quarta parte de uma circunferência é :
Então temos que:
Como a área é numericamente igual a integral, temos:
Resposta
(a) 30
(b) 0
(c)
(d)