Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 14
14. Determine o volume do sólido gerado pela rotação em torno do eixo da região limitada por , , e . (A região está situada nos primeiro e terceiro quadrantes, e assemelha-se a uma gravata-borboleta inclinada.)
Passo 1
Se nós desenharmos a função vamos ver que ela é dessa forma:
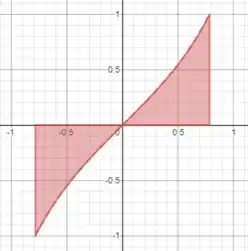
Usando o método do disco essa questão fica simples de resolver.
O raio do disco é igual ao valor da função ,
perceba que não importa se o valor da função é negativo ou positivo, quando calculamos a área do disco esse valor é elevado ao quadrado:
Por fim, para descobrirmos o volume só precisamos aplicar a área na fórmula:
Vamos usar a identidade trigonométrica
e reescrever a equação:
Integral de 1 é e a integral de é , então o volume fica:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 25 - x 2 ,y = 0 ,x =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. y = x 3 ; y = x ; x ≥ 0 ; Em torno do eixo x .
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x 2 / 3 ,x = 1 ,y =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y 2 = x ,x = 2 y ;e mt o
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 x ,y = 0 , x = 1 ,