Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 18

Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos.

y = x ,   y = 0 ,   x = 2 ,   x = 4 ;           e m   t o r n o   d e   x = 1

Passo 1

Opa, bora resolver esse problema! Temos uma região limitada pelas seguintes curvas:

y = x ,   y = 0 ,   x = 2 ,   x = 4

Se a gente rotacionar essa região em torno do eixo x   obtemos um sólido. O enunciado pede pra a gente encontrar o volume edsse sólido! Para isso vamos usar a seguinte fórmula:

V = ∫ a b A x d x

Além disso precisamos esboçar a região, o sólido e um disco ou arruela típicos que respresente a secção transversal!

Vamos colocar a mão na massa!

Passo 2

Vamos começar desenhando a região delimitada pelas curvas:

y = x

  y = 0

x = 2

  x = 4

Temos que a área é representada pela figura abaixo:

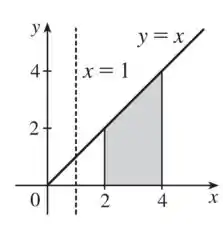
Passo 3

Quando rotacionarmos a área acima temos um volume com secção transversal circular e o seu raio vai ser igual a:

x = 4 - 1

  x = 2 - 1

Percebe que aqui a gente tem dois “raios”. Um interno e um exerno! Além disso a gente pegou a função dada e diminuiu de 1 , que é o eixo de rotação!

Agora vamos esboçar o sólido e a arruela:

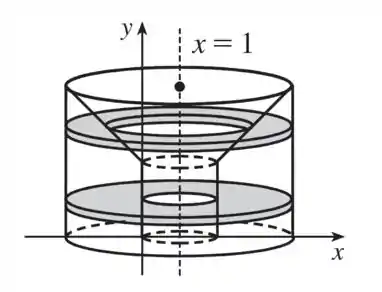
Essas regiões sombreadas são discos que representam secções transversais do sólido!

Observando esse gráfico percebemos que os limites de integração são: a = 0 e b = 2 , a = 2 e b = 4 .Isso mesmo, vamos separar a integral em duas! Uma correspondente a essa parte cilíndrica e outra a parte cônica.

Além disso nesse caso vai ser mais interessante integrar com respeito a y .

Passo 4

Utilizando a definição de volume de sólido de revolução, podemos escrever a seguinte integral

V = ∫ 0 2 π [ 4 - 1 2 - 2 - 1 2 ] d y + ∫ 2 4 π [ 4 - 1 2 - y - 1 2 ] d y

Resolvendo a integral, temos:

V = π 8 y 0 2 + ∫ 2 4 π 8 + 2 y - y 2 d y = 16 π + π 8 y + y 2 - y 3 3 2 4

V = 16 π + π 32 + 16 - 64 3 - 16 + 4 - 8 3

V = 76 3 π

Prontinho!

Resposta

V = 76 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46. A base de um sólido é a região encerrada por um círculocom um raio de r unidades, e todas as secções planas perpendiculares a um diâmetro fixo da base são triângulos retângulos isósceles, com a hi
45. A base de um sólido é a região a região do Exercício 43. Ache o volume do sólido se todas as secções planas perpendiculares a um diâmetro fixo da base forem triângulos isósceles de altura igual à
44. A base de um sólido é a região encerrada por um círculo com raio de 4 cm de raio, e cada seção plana perpendicular a um diâmetro fixo da base é um triângulo isósceles com 10 cm de altura e uma cor
48. Dois cilindros circulares retos, cada um tendo um raio de r unidades, têm seus eixos interceptando-se em ângulos retos. Ache o volume do sólido comum aos dois cilindros.
46. Resolva o Exercício 46, se os triângulos retângulos isósceles tiverem um dos catetos no plano da base.