Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 15
15. Volume de um orifício de uma esfera sólida Um orifício redondo de raio pés é furado através do centro de uma esfera sólida de raio 2 pés. Determine o volume de material removido da esfera.
Passo 1
Imagine uma esfera com a seção transfersal dessa forma:
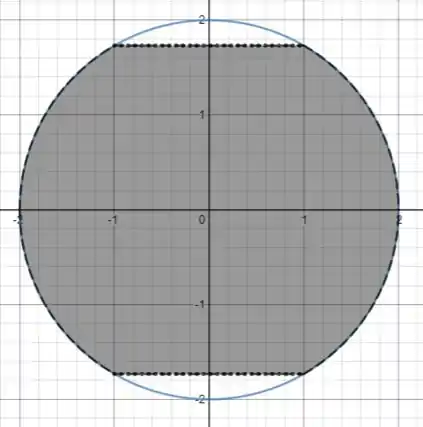
A parte preta foi a parte tirada da esfera.
Para calcularmos o volume que foi removido vamos calcular o volume que sobrou e subtrai-lo do volume total da esfera.
O volume que sobrou pode ser calculado a partir da revolução dessa área azul:
Passo 2
Nós vamos usar o método do anel para descobrirmos esse volume, para isso precisamos do raio externo e do raio interno:
O raio interno vai ser :
Já o raio externo vai ser o valor da função da circunfêrencia, então precisamos achá-la.
A função de uma cincunferência qualquer é igual a
No nosso caso o raio vale , então
Precisamos da coordenada para descobrirmos o raio do nosso disco:
Porém vamos usar só a coordenada positiva
Então
Para aplicarmos na fórmula:
só falta descobrir e :
Eles são os valores de quando , calculando esses valores:
Portanto e , aplicando tudo na fórmula:
Passo 3
O volume total de uma esfera é igual a
O raio dessa esfera é 2, então:
Então o volume retirado foi: