Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 55
Esboce as parábolas nos Exercícios 55-58. Inclua o foco e a diretriz em cada esboço.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de equações paramétricas e coordenadas polares.
Vamos agora resolver os exercícios práticos sobre desenhos de secções cônicas.
Lembrando que a equação da parábola é:
E comparando com a equação fornecida, temos que:
Logo, o foco e a diretriz são dados, respectivamente por:
Passo 2
O esboço da parábola fica:
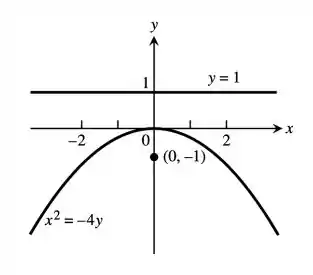
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.
Resposta
Ver passo a passo.
Exercícios de Livros Relacionados
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.45. r 2 = - 4 rc o s θ
Represente graficamente os pontos (dados em coordenadas polares). Em seguida, encontre todas as coordenadas polares de cada um dos pontos.a. ( 2 , π / 2 ) b. ( 2,0 ) c. ( - 2 , π / 2 ) d. ( - 2,0 )
Quais pares de coordenadas polares representam o mesmo ponto?a. ( - 2 , π / 3 ) b. ( 2 , π / 3 ) c. ( r , θ ) d. ( r ,θ + π ) e. ( - r , θ ) f. ( 2 , - 2 π / 3 ) g. ( - r ,θ + π ) h. ( - 2,2 π / 3 )
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.38. r2 s e n2 θ = 2
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.32. r=- 3 s e cθ