Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 61

Encontre as excentricidades das elipses e hipérboles nos Exercícios 59-62. Esboce cada seção cônica. Inclua os focos, vértices e assíntotas (conforme apropriado) em seu esboço.

3 x 2 - y 2 = 3

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de equações paramétricas e coordenadas polares.

Vamos agora resolver os exercícios práticos sobre desenhos de secções cônicas.

Lembrando que a equação da hipérbole é:

x 2 a 2 - y 2 b 2 = 1

Devemos escrever a equação fornecida no formato acima lembrado, dividindo a equação toda por 3:

3 x 2 3 - y 2 3 = 3 3 = > x 2 - y 2 3 = 1

Daí temos que:

a 2 = 1 = > a = 1   e   b 2 = 3 = > b = 3

Sabemos também que:

c 2 = a 2 + b 2 ,   o u   s e j a ,   c 2 = 1 + 3 = 4 = > c = 2

E a excentricidade é dada por:

e = c a = 2 1 = 2

Devemos lembrar ainda, que as assíntotas são dadas por:

y = ± b a x ,   o u   s e j a ,   y = ± 3 1 x = ± 3 x

Passo 2

O esboço da hipérbole fica:

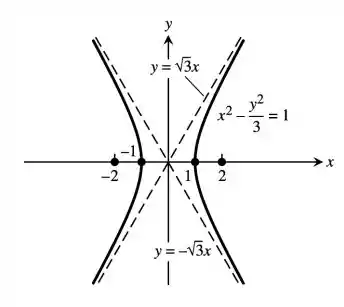
E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.27. r c o s θ = 2
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.34. rc o sθ = rs e nθ
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.30. rc o sθ = 0
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.31. r c o s θ + rs e nθ = 1
Substitua as equações polares nos Exercícios 27-52 por equações cartesianas equivalentes. Em seguida, descreva ou identifique o gráfico.41. r = c o s s e cθ e r c o sθ