Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.7 - Ex. 14
14.
(a) Examinando os gráficos de em função de nas Figuras 9.7.3, 9.7.5 e 9.7.7, estime o período do oscilador de van der Pol nesses casos.
(b) Calcule e faça o gráfico das soluções da equação de van der Pol para outros valores do parâmetro . Estime o período também nesses casos.
(c) Faça o gráfico dos valores estimados de em função de. Descreva como depende de .
Passo 1
Bem, aqui basta a gente olhar novamente para esses gráficos e fazer uma estimativa dos valores do período. Lembre-se de que o período é o menor tempo que descreve um padeço da onda que se repete formando toda onda (comprimento de onda).
Olhando atentamente para essas figuras no livro, pode se fazer uma estimativa do período para cada uma ficando com essa tabela resumo aqui:
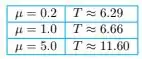
Passo 2
- Para um valor de e condições iniciais e temos...
- Para e as mesmas condições iniciais...
- Para ...
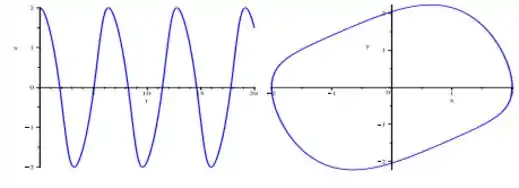
Onde conseguimos verificar um período de , aproximadamente.
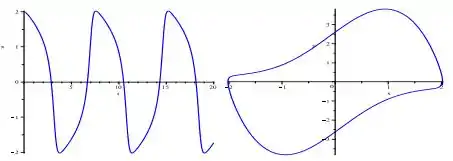
O período aqui é aproximadamente
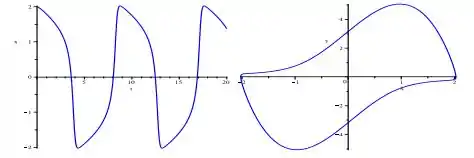
O período é de maios ou menos
Passo 3
Com esses períodos em mãos e os valores de que o geraram, podemos gerar um gráfico de :
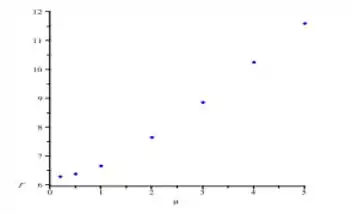
E perceba que eles possuem uma relação meio que de um paraboloide: isso significa que aparentemente varia proporcional , saca?
Resposta
Ei, a resposta está no passo a passo :)