17. Considere o sistema de van der Pol
em que permitimos agora que μ seja qualquer número real.
(a) Mostre que a origem é o único ponto crítico. Determine seu tipo e propriedades de estabilidade, e como eles dependem de .
(b) Seja ; desenhe um retrato de fase e conclua que existe uma solução periódica contendo a origem em seu interior. Note que essa solução periódica é instável. Compare seu gráfico com a Figura 9.7.4.
(c) Desenhe um retrato de fase para alguns outros valores negativos de . Descreva como a forma da solução periódica varia com.
(d) Considere valores de pequenos em módulo, positivos ou negativos. Desenhando retratos de fase, determine como a solução periódica varia quando . Compare o comportamento do sistema de van der Pol quando aumenta passando por zero com o comportamento do sistema no Problema 16.
Passo 1
Para encontramos o ou os pontos críticos, devemos igualar as derivadas a no nosso sistema:
Repare então que da primeira equação na segunda...
Isso basicamente significa de fato que o único ponto crítico .
Passo 2
Beleza! Então para discutir sobre a estabilidade primeiro montemos o nosso sistema localmente linear removendo as informações de quem são e :
Agora encontremos a jacobiana disso:
Substituindo o ponto ...
Então o sistema localmente linear será...
Para provar essa questão estabilidade, vamos ter que buscar os autovalores da matriz:
Então...
Resolvendo essa equação do segundo grau...
VEJAMOS PRIMEIRO A CONDIÇÃO DE QUE
Nessa condição, será um número positivo, mas a raiz dele será levemente menor que , de modo que, mesmo somando, o resultado de ainda será negativo, logo teremos uma estabilidade assintótica e será um ponto nodal.
VEJAMOS AGORA A CONDIÇÃO DE QUE :
Nessa condição , então teremos dois autovalores imaginários com a parte real , negativa e, portanto, o sistema será estável em espiral.
VEJAMOS AGORA A CONDIÇÃO DE QUE :
Nessa condição , então teremos dois autovalores imaginários com a parte real , positiva e, portanto, o sistema será instável em espiral.
VEJAMOS AGORA A CONDIÇÃO DE QUE :
Nesse caso, os valores de são reais e positivos, logo, gerará um ponto de instabilidade.
Passo 3
Para resolver esse problema daqui, precisamos de programação, afinal devemos resolver o sistema não linear considerando :
Aqui, como o problema não deixa específico que tipo de programação usar, você pode resolver como bem entender. Eu vou utilizar a linguagem MATLAB:

O meu código está comentado, caso você queira copiar e estuda-lo, mas já adianto que não tem muito segredo, já que o MATLAB já nos define uma função que nos resolve sistemas de EDO: “ode45”.
Essa função depende de da definição das EDO’s que eu programei em uma função:

Perceba eu criei 5, soluções, duas que começam nos pontos e e outras 3 que começam nos pontos , e . As duas primeiras estão plotadas em vermelho e as outras três em azul:
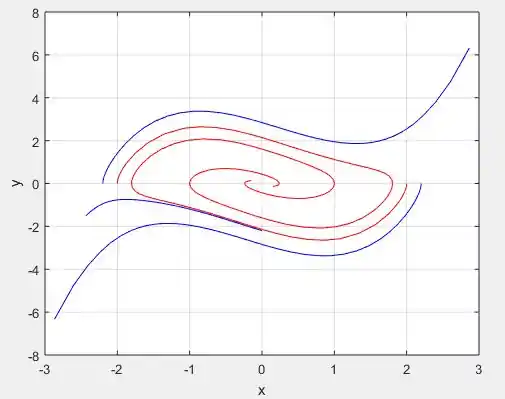
Esse é o retrato de fase das soluções e perceba que de fato existe uma solução periódica que contem o centro, já que as curvas tendem a se concentrar nas bordas desse “bolinho”. Além disso, perceba que de fato essa solução periódica é instável, pois qualquer ponto que comece próximo de , ora vão para o infinito, como as azuis, ou vão para o centro, como as vermelhas!
Passo 4
Mudando a função na função para alguns outros valores e plotando o mesmo gráfico:
- Para
- Para
- Para
- Para ...
- Para ...
- Para ...
- Para ...

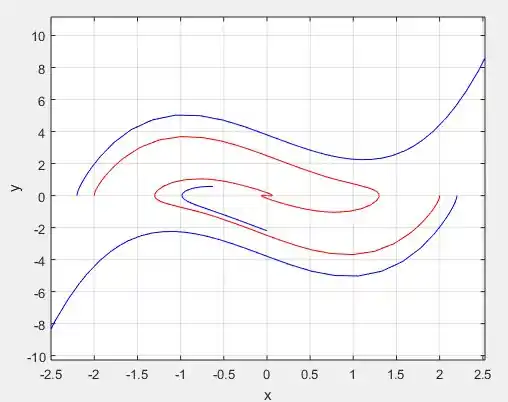
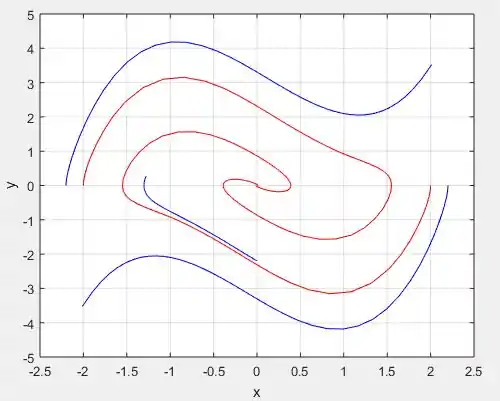
Para

Perceba que a medida que vamos reduzindo , as curvas ficam mais concêntricas!
Passo 5
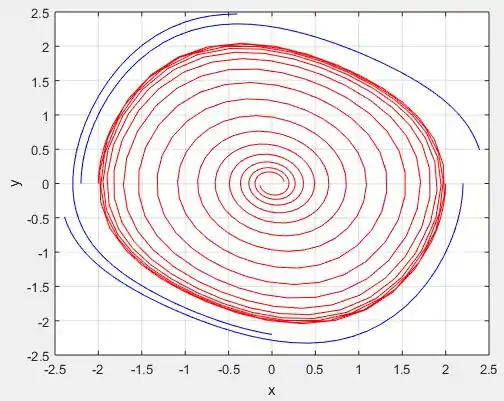
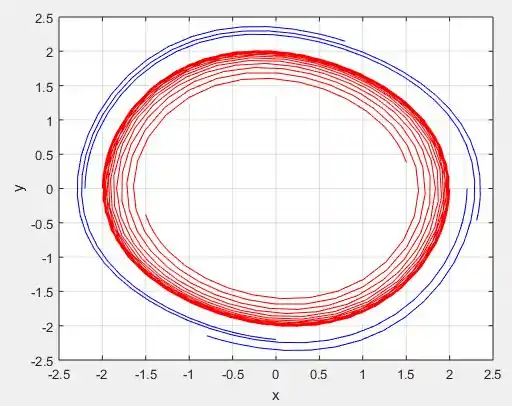
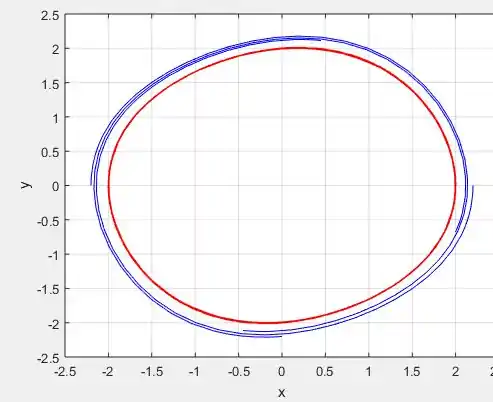
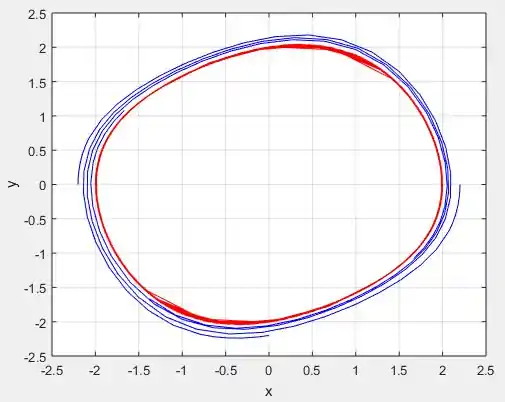
Perceba que de fato, quanto mais próximo de , cada vez mais vamos deixando de ter espirais e vamos tendo um formato de círculo centrado na origem .
Resposta
Ei, a resposta está no passo a passo :)