Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.7 - Ex. 19

19. Considere o sistema

x ' = x a - 0,2 x - 2 y x + 6 ,         y ' = y - 0,25 + x x + 6

Em que a é um parâmetro positivo. Note que esse sistema inclui o do Problema 18 acima e também o do Problema 13 na Seção 9.5.

(a) Encontre todos os pontos críticos.

(b) Considere o ponto crítico no interior do primeiro quadrante. Encontre os autovalores do sistema linear aproximado. Determine o valor a 0 em que esse ponto crítico muda de assintoticamente estável para instável.

(c) Desenhe um retrato de fase para um valor de a ligeiramente maior do que a 0 . Observe que aparece um ciclo limite. Como esse ciclo limite varia quando a aumenta mais?

Passo 1

L e t r a   A :

Para encontrar tais pontos como já estamos acostumados, a primeira coisa a se fazer é zerar as derivadas:

0 = x a - 0,2 x - 2 y x + 6 ,         0 = y - 0,25 + x x + 6   →

Jogando esse sisteminha no WolframAlpha para ganharmos tempo, já que a questão nos permite o auxílio de um computador, ganharemos a seguinte resposta:

x = 0       e         y = 0       →               0 ,   0

x = 2       e         y = 4 a - 8 5       →               2 ,   4 a - 8 5

x = 5 a       e         y = 0       →               5 a ,   0

Então todos esses são pontos críticos! Saca?

Passo 2

L e t r a   B :

O ponto crítico no interior do primeiro quadrante é

2 ,   4 a - 8 5

Para encontrar os autovalores do sistema linear aproximado e depois encontrar a 0 , devemos...

x ' = x a - 0,2 x - 2 y x + 6                           →                 F x ,   y = a x - 0,2 x 2 - 2 y x x + 6

y ' = y - 0,25 + x x + 6                                   →                 G x ,   y = - 0,25 y + x x + 6 y

Agora encontremos a jacobiana disso:

J x ,   y = F x F y G x G y     →

J x ,   y = a - 2 ⋅ 0,2 x - 2 y x + 6 - 2 y x x + 6 2 - 2 x x + 6 y x + 6 - y x x + 6 2 - 0,25 + x x + 6       →

Substituindo o ponto de interesse 2 ,   4 a - 8 5 ...

J 2 ,   4 a - 8 5 = a - 2 ⋅ 0,2 ⋅ 2 - 2 ⋅ 4 a - 8 5 2 + 6 - 2 ⋅ 4 a - 8 5 ⋅ 2 2 + 6 2 - 4 2 + 6 4 a - 8 5 2 + 6 - 4 a - 8 5 ⋅ 2 2 + 6 2 - 0,25 + 2 2 + 6    

Simplificando isso aí...

J 2 ,   4 a - 8 5 = a - 0,8 - 2 ⋅ 4 a - 8 5 8 - 16 a + 32 5 64 - 1 2 4 a - 8 5 8 - 8 a - 16 5 64 - 0,25 + 1 4    

SIMPLIFICANDO AINDA MAIS...

J 2 ,   4 a - 8 5 = a 4 - 1 2 - 1 2 3 a 8 - 3 20 0    

Então o sistema localmente linear será...

x ' y ' = a 4 - 1 2 - 1 2 3 a 8 - 3 20 0 x - 2 y - 4 a - 8 5

Para estudar a estabilidade e o tipo de ponto venha comigo calcular os autovetores!

Passo 3

Vamos começar avaliando o ponto 2 ,   4 a - 8 5 , ok? Para isso vamos pegar aqui a matriz jacobiana desse ponto, como vimos no passo anterior...

M = a 4 - 1 2 - 1 2 3 a 8 - 3 20 0   →

Calculando então os autovalores dessa matriz...

det ⁡ M - r I = 0

det ⁡ a 4 - 1 2 - r - 1 2 3 a 8 - 3 20 - r = 0 →

a 4 - 1 2 - r - r + 1 2 3 a 8 - 3 20 = 0   →

Simplificando essa equação...

- a 4 - 1 2 r + r 2 + 3 a 16 - 3 40 = 0   →

r 2 - a 4 - 1 2 r + 3 a 16 - 3 40 = 0   →

Resolvendo essa equação do segundo grau...

r = + a 4 - 1 2 2 ± a 4 - 1 2 2 - 4 3 a 16 - 3 40 2    

O valor de a 0 que mudará então de estável para instável e de tal modo que zere esse valor real:

a 4 - 1 2 2 = 0     →

Então...

a 0 = 2

Saca? Se a for menor que 2 , o valor de r vai ter uma parte real positiva (sistema instável), e se ele for menor o sistema será estável.

Passo 4

L e t r a   C :

Usando o mesmo código da questão anterior, só mudando a equação de definição do nosso sistema de EDO para o as nossas equações atuais:

x ' = x a - 0,2 x - 2 y x + 6 ,         y ' = y - 0,25 + x x + 6

Dessa forma aqui:

E escolhendo alguns pontos iniciais, como o ponto 1 ,   1 ou 11 ,   1 , e principalmente a = 2,05   perceba que sempre as trajetórias tem a essa concha:

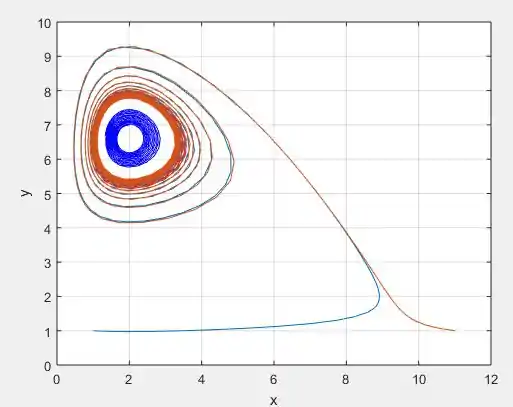
Observe que de fato aparecem cada vez mais círculos limites para a solução, pelo menos mais parecidas com círculos. Se começarmos a aumentar ainda mais o a , digamos, para 3 ...

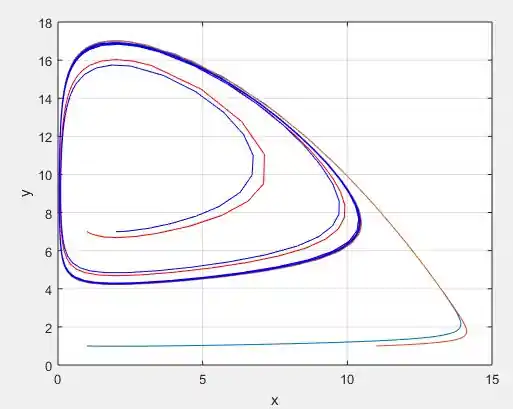
Observe que embora as soluções continuem convergindo para a periodicidade, não é mais um círculo e sim essa espécie de concha!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8. (a) Para r=21 , faça os gráficos de x em função de t para as soluções com pontos iniciais ( 3 ,8 ,0 ) , ( 5 ,5 ,5 ) e ( 5 ,5 ,10 ) . Use um intervalo para t de, pelo menos,0≤t≤30 . Compare seus grá
8. (a) Para r=21 , faça os gráficos de x em função de t para as soluções com pontos iniciais ( 3 ,8 ,0 ) , ( 5 ,5 ,5 ) e ( 5 ,5 ,10 ) . Use um intervalo para t de, pelo menos,0≤t≤30 . Compare seus grá
10. Considere, agora, valores de r ligeiramente maiores do que os no Problema 9.(a) Faça o gráfico de trajetórias das equações de Lorenz para valores de r entre 100 e 100,78 . Você deveria observar um
9. Em determinados intervalos para r , as equações de Lorenz exibem uma propriedade de duplicação do período semelhante ao que ocorre na equação de diferenças logística discutida na Seção 2.9. Cálculo
14.(a) Seja c=3 . Encontre os pontos críticos e os autovalores correspondentes.(b) Desenhe a trajetória que começa no ponto ( 1 ,0 ,- 2 ) . Observe que o ciclo limite agora consiste em dois laços ante