Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.7 - Ex. 18

18. Considere o sistema

x ' = x 2,4 - 0,2 x - 2 y x + 6 ,         y ' = y - 0,25 + x x + 6

Note que esse sistema só difere do sistema no Problema 13 da Seção 9.5 na taxa de crescimento da presa.

(a) Encontre todos os pontos críticos.

(b) Determine o tipo e as propriedades de estabilidade de cada ponto crítico.

(c) Desenhe um retrato de fase no primeiro quadrante e conclua que existe um ciclo limite assintoticamente estável. Assim, esse modelo prevê uma oscilação estável em longo prazo das populações da presa e do predador.

Passo 1

L e t r a   A :

Para encontrar tais pontos como já estamos acostumados, a primeira coisa a se fazer é zerar as derivadas:

0 = x 2,4 - 0,2 x - 2 y x + 6 ,         0 = y - 0,25 + x x + 6   →

Jogando esse sisteminha no WolframAlpha para ganharmos tempo, já que a questão nos permite o auxílio de um computador, ganharemos a seguinte resposta:

x = 0       e         y = 0       →               0 ,   0

x = 2       e         y = 8       →               2 ,   8

x = 12       e         y = 0       →               12 ,   0

Então todos esses são pontos críticos! Saca?

Passo 2

L e t r a   B :

Beleza! Então para discutir sobre a estabilidade primeiro montemos o nosso sistema localmente linear removendo as informações de quem são F e G :

x ' = x 2,4 - 0,2 x - 2 y x + 6                           →                 F x ,   y = 2,4 x - 0,2 x 2 - 2 y x x + 6

y ' = y - 0,25 + x x + 6                                   →                 G x ,   y = - 0,25 y + x x + 6 y

Agora encontremos a jacobiana disso:

J x ,   y = F x F y G x G y     →

J x ,   y = 2,4 - 2 ⋅ 0,2 x - 2 y x + 6 - 2 y x x + 6 2 - 2 x x + 6 y x + 6 - y x x + 6 2 - 0,25 + x x + 6       →

  • Substituindo o ponto 0 ,   0 ...

    • J 0 ,   0 = 2,4 0 0 - 0,25  

    Então o sistema localmente linear será...

    x ' y ' = 2,4 0 0 - 0,25 x y

  • Substituindo o ponto 2 ,   8 ...

    • J 2 ,   8 = 2,4 - 2 ⋅ 0,2 ⋅ 2 - 2 ⋅ 8 2 + 6 - 2 ⋅ 8 ⋅ 2 2 + 6 2 - 4 2 + 6 8 2 + 6 - 8 ⋅ 2 2 + 6 2 - 0,25 + 2 2 + 6  

    Então o sistema localmente linear será...

    x ' y ' = 0,1 - 0,5 0,75 0 x - 2 y - 8

  • Substituindo o ponto 12 ,   0 ...

J 2 ,   8 = 2,4 - 2 ⋅ 0,2 ⋅ 1 2 - 2 ⋅ 12 12 + 6 0 - 0,25 + 1 2 1 2 + 6  

Então o sistema localmente linear será...

x ' y ' = - 2,4 - 4 / 3 0 - 0,25 + 2 / 3 x - 12 y

Para estudar a estabilidade e o tipo de ponto, vamos separar em três passos diferentes, cada um para avaliar um ponto!

Passo 3

Vamos começar avaliando o ponto 0 ,   0 , ok? Para isso vamos pegar aqui a matriz jacobiana desse ponto, como vimos no passo anterior...

M = 2,4 0 0 - 0,25   →

Calculando então os autovalores dessa matriz...

det ⁡ M - r I = 0

det ⁡ 2,4 - r 0 0 - 0,25 - r = 0 →

2,4 - r - 0,25 - r = 0   →

r 1 = 2,4         e           r 2 = - 0,25

Logo, como um dos autovalores foi positivo, o sistema é instável próximo desse ponto crítico!

Passo 4

Agora vamos fazer a mesma análise, mas dessa vez para o ponto 2 ,   8 . Pegando a matriz Jacobiana correspondente...

M = 0,1 - 0,5 0,75 0   →

det ⁡ M - r I = 0

det ⁡ 0,1 - r - 0,5 0,75 - r = 0 →

0,1 - r - r + 0,375 = 0   →

r 1 = 0.5 + 0.610328 i       e           r 2 = 0.5 - 0.610328 i

Logo, como os autovalores são imaginários onde o a parte real é positiva, o sistema é instável próximo desse ponto crítico e é formado por espirais!

Passo 5

Por último, vamos fazer a mesma análise do ponto 1 2 ,   0 . Pegando a matriz Jacobiana correspondente...

M = - 2,4 - 4 / 3 0 - 0,25 + 2 / 3   →

det ⁡ M - r I = 0

det ⁡ - 2,4 - r - 4 / 3 0 - 0,25 + 2 3 - r = 0 →

- 2,4 - r - 0,25 + 2 3 - r = 0   →

r 1 = - 2,4       e           r 2 = - 0,25 + 2 3

Logo, como um dos autovalores foi positivo, o r 2 , o sistema é instável próximo desse ponto crítico!

Passo 6

L e t r a   C :

Usando o mesmo código da questão anterior, só mudando a equação de definição do nosso sistema de EDO para o as nossas equações atuais:

x ' = x 2,4 - 0,2 x - 2 y x + 6 ,         y ' = y - 0,25 + x x + 6

Dessa forma aqui:

E escolhendo alguns pontos iniciais, como o ponto 1 ,   1 ou 11 ,   1 , perceba que sempre as trajetórias tem a essa concha:

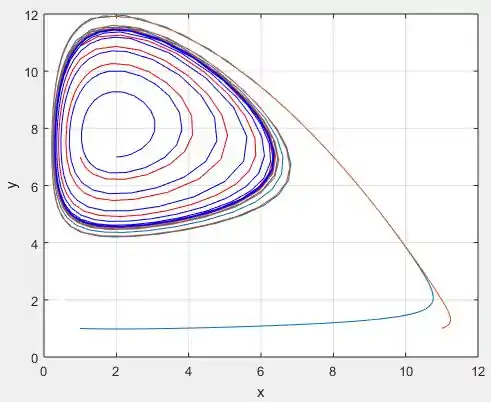
Provando que em algum momento de fato a solução vai começar a girar e se tornar periódica!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2. (a) Mostre que a aproximação linear válida perto do ponto crítico P 2 é dada pela Eq. (11).(b) Mostre que os autovalores do sistema (11) satisfazem a Eq. (12).(c) Para r=28 , resolva a Eq. (12) e d
Em cada um dos problemas de 6 a 10, faça as investigações pedidas sobre as equações de Lorenz.6. Para r=28 , faça o gráfico de x em função de t para os casos ilustrados nas Figuras 9.8.2 e 9.8.3. Seus
4. Use a função de Liapunov V x ,y ,z = x 2 + σ y 2 + σ z 2 para mostrar que a origem é um ponto crítico global assintoticamente estável para as equações de Lorenz (1) se r1 .
3.(a) Resolvendo a Eq. (12) numericamente, mostre que a parte real das raízes complexas muda de sinal quando r≅24,737 .(b) Mostre que um polinômio de grau três da forma x 3 + A x 2 + B x + C tem uma r
8. (a) Para r=21 , faça os gráficos de x em função de t para as soluções com pontos iniciais ( 3 ,8 ,0 ) , ( 5 ,5 ,5 ) e ( 5 ,5 ,10 ) . Use um intervalo para t de, pelo menos,0≤t≤30 . Compare seus grá