Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 14-d

14. Suponha que determinada população tem uma taxa de crescimento que varia com o tempo e queessa população satisfaz a equação diferencial

dy/dt =(0,5 + sen t)y/5.

(a) Se y(0) = 1, encontre (ou estime) o instante τ no qual a população dobrou. Escolha outrascondições iniciais e determine se o tempo de duplicação τ depende da população inicial.(b) Suponha que a taxa de crescimento é substituída pelo seu valor médio 1/10. Determine otempo de duplicação τ nesse caso.(c) Suponha que o termo sen t na equação diferencial é substituído por sen(2πt); ou seja, avariação na taxa de crescimento tem uma frequência substancialmente mais alta. Qual o efeitodisto no tempo de duplicação τ?(d) Faça o gráfico das soluções obtidas nos itens (a), (b) e (c) em um único conjunto de eixos.

Passo 1

Vamos reunir tudo o que já calculamos ate agora e fazer os gráficos das soluções tudo no mesmo eixo

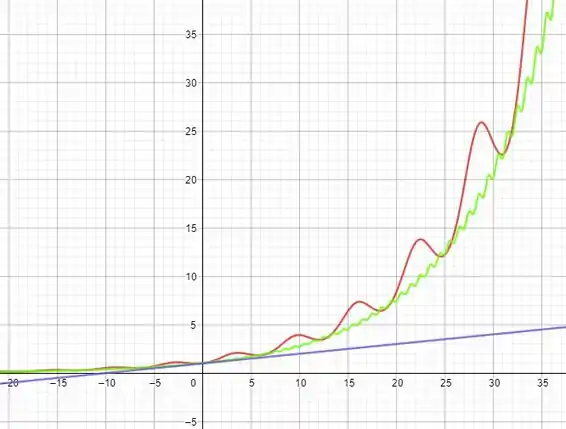
Onde a curva vermelha é nossa função da letra a)

A curva azul é nossa função da letra b)

E por fim , a curva verde é a letra c)

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A matrícula em certa universidade vem crescendo a uma taxa de 1000 1 + t - 1 / 2 estudantes por ano desde 1985. Se a matrícula em 1988 foi de 10000:a)qual foi a matrícula em 1985

A função rendimento marginal para certo artigo é dada por R ' x = 3 4 x 2 - 10 x + 12 .a)Ache a função do rendimento total.

A matrícula em certa universidade vem crescendo a uma taxa de 1000 1 + t - 1 / 2 estudantes por ano desde 1985. Se a matrícula em 1988 foi de 10000:b)qual será a matrícula em 1993 se é esperado que el

A função rendimento marginal para certo artigo é dada por R ' x = 3 4 x 2 - 10 x + 12 .b)Ache uma equação envolvendo p e x (equação de demanda), onde x unidades são demandadas quando p for o preço por

O volume de um balão está crescendo de acordo com a fórmula d V d t = t + 1 + 2 3 t , onde V em cm³ é o volume do balão em t s. Se V = 33 quando t = 3 , ache:b)O volume do balão em 8 s.