Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 44
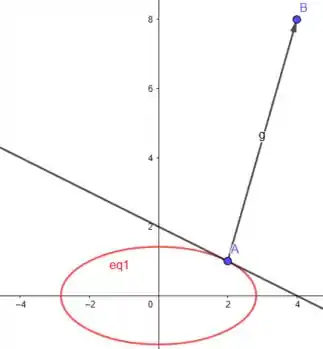
14.47. Se , determine o vetor gradiente e use-o para determinar a reta tangente à curva de nível da função no ponto . Esboce as curvas de nível, reta tangente e vetor gradiente.
Passo 1
Beleza, vamos lá...
Aqui nós temos a função
e queremos determinar o vetor gradiente de no ponto Depois disso, vamos usar esse vetor para determinar a reta tangente à curva de nível da função no ponto
Temos que determinar o vetor gradiente, e a gente o calcula assim:
O gradiente da função em um certo ponto acaba sendo perpendicular à curva de n��vel da função que contém aquele ponto. Então, se queremos a reta tangente à curva de nível no ponto , ela será perpendicular ao gradiente de nesse ponto.
Dessa forma, qualquer vetor que dê a direção da reta será perpendicular ao gradiente. Por exemplo, o vetor é um vetor paralelo à reta. Assim,
Dessa equação nós teremos todos os pontos da reta e ela estará determinada.
Tranquilo? Vem comigo que eu te mostro como finalizar essa questão agora.
Passo 2
Vamos começar calculando o gradiente de :
e
Logo,
Ou seja, no ponto o gradiente é:
Passo 3
Para nos ajudar a entender, vamos visualizar a curva de nível pedida, .
Se dividirmos ambos os lados por 8, obtemos
Vamos escrever com uma cara mais conhecida:
Essa é a equação de uma elipse! Portanto, a curva de nível pedida é uma elipse no plano .
Vejamos como fica essa curva e o gradiente que calculamos:
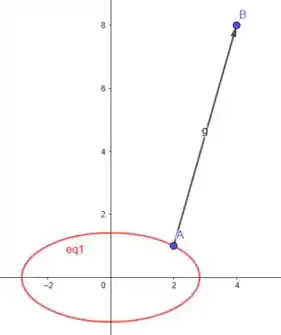
onde e .
Passo 4
Agora vamos obter a equação da reta tangente à curva de nível no ponto
Como discutido, o vetor é um vetor paralelo à reta. Assim,
Escrevendo a equação acima para o ponto obtemos
Abrindo os termos:
Logo,
É a reta tangente à curva no ponto Vejamos como fica essa reta de fato:
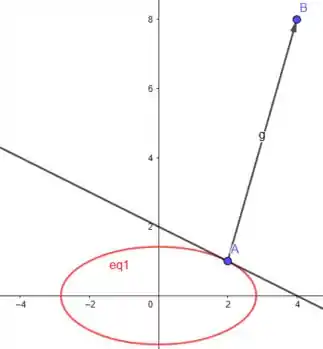
Resposta
