14.
(a) Seja . Encontre os pontos críticos e os autovalores correspondentes.
(b) Desenhe a trajetória que começa no ponto . Observe que o ciclo limite agora consiste em dois laços antes de fechar; é chamado muitas vezes de 2-ciclo.
(c) Faça o gráfico de x, y ou z em função de t e mostre que o período T2 de movimento no 2- ciclo está muito próximo do dobro do período do ciclo limite simples no Problema 12. Ocorreu uma bifurcação com duplicação de período dos ciclos para algum valor de c entre e .
Passo 1
A primeira coisa que devemos aqui é substituir as derivadas por , já que estamos buscando os valores dos pontos críticos:
Da segunda equação...
E da primeira equação, tiramos que...
Jogando esses dois últimos resultados na última equação...
Poxa! Uma equação do segundo grau:
Substituindo então o por e resolvendo a equação do segundo grau...
BELEZA! Substituindo então nas informações de e de ...
Os dois pontos críticos nesse caso então serão...
O jacobiano desse primeiro ponto será então...
Jogando no Wolfram para obter seus autovalores ganharemos...
MAS CALMA, meu Jovem! Temos um segundo ponto crítico e que certamente precisa ser avaliado também!
Calculando os seus autovalores por sua vez obteremos...
Passo 2
Usando o mesmo código então do exercício 11, mas mudando o ponto inicial para o ponto pedido: e considerando o , aqui está o gráfico da solução...
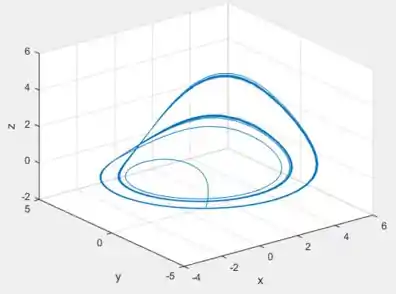
Observe que de fato a solução tem 2 voltas hehe!
Passo 3
Bem, no problema 12, encontramos um período de . Aqui, fazendo o gráfico de e todos juntos do mesmo jeito que fizemos lá nesse problema...
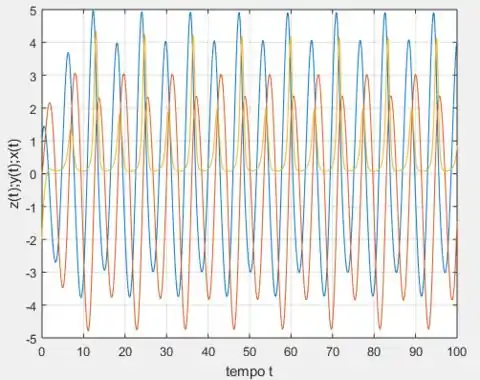
Observe que de fato entre dois mínimos da curva laranja, de fato temos um intervalo de , sugerindo que o período dobrou de para .
Resposta
Ei, a resposta está no passo a passo :)