Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 15
15.
(a) Seja . Encontre os pontos críticos e os autovalores correspondentes.
(b) Desenhe a trajetória que começa no ponto . Observe que o ciclo limite agora é um 4-ciclo. Encontre o período T4 do movimento. Ocorreu outra bifurcação com duplicação de período para c entre e .
(c) Para, mostre que o ciclo limite é um 8-ciclo. Verifique se seu período está muito próximo de oito vezes o período do ciclo limite simples no Problema 12.
Nota: À medida que c continua aumentando, há uma sequência acelerada de bifurcações com duplicação de período. Os valores de bifurcação de c convergem para um limite que marca o início do caos.
Passo 1
A primeira coisa que devemos aqui é substituir as derivadas por , já que estamos buscando os valores dos pontos críticos:
Da segunda equação...
E da primeira equação, tiramos que...
Jogando esses dois últimos resultados na última equação...
Poxa! Uma equação do segundo grau:
Substituindo então o por e resolvendo a equação do segundo grau...
BELEZA! Substituindo então nas informações de e de ...
Os dois pontos críticos nesse caso então serão...
O jacobiano desse primeiro ponto será então...
Jogando no Wolfram para obter seus autovalores ganharemos...
MAS CALMA, meu Jovem! Temos um segundo ponto crítico e que certamente precisa ser avaliado também!
Calculando os seus autovalores por sua vez obteremos...
Passo 2
Usando o mesmo código então do exercício 11, mas mudando o ponto inicial para o ponto pedido: e considerando o , aqui está o gráfico da solução no 3D, bem como os gráficos de , e feito no exercício anterior...
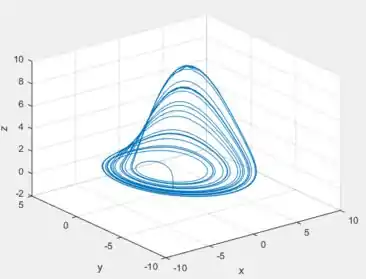
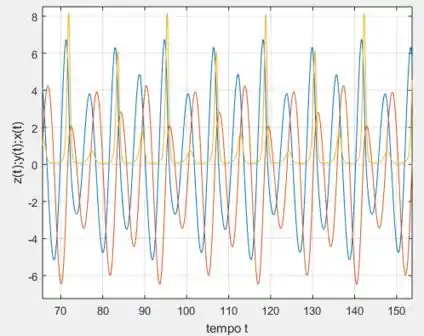
Da primeira figura a gente consegue ver aproximadamente 4 ciclos, neh?
E a segunda figura apenas confirma que de fato o período agora quadriplicou em relação ao exercício 12, pois os pontos de mínimo da função em laranja acontece mais ou menos entre o tempo , e depois só volta acontecer em , sugerindo um período de , ou .
Passo 3
Fazendo os mesmos gráficos agora, mas para agora para ...
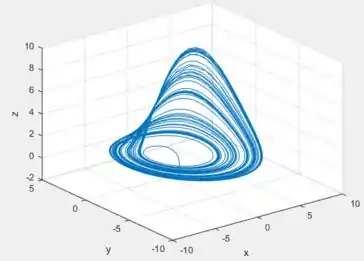
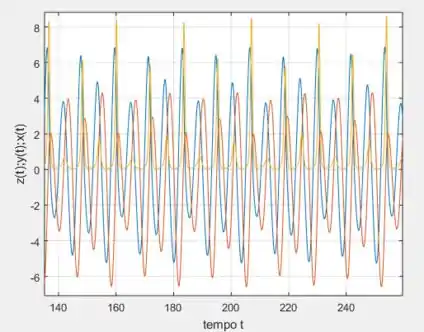
A interpretação dessas figuras aqui já é menos intuitiva que as do passo anterior, mas ainda assim, veja pelos valores máximos da função amarela que há uma diferença de aproximadamente , observe isso entre esses dois pontos de máximo aqui, oh:
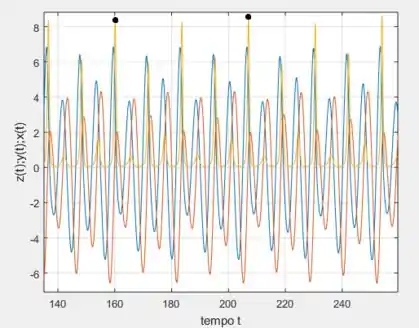
Os pontos que marcam isso são os pretinhos ! De fato, , sugerindo que o período foi multiplicado por , nesse caso .
Resposta
Ei, a resposta está no passo a passo :)